题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式.
【答案】
(1)解:由a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*,令n=1,则S2﹣2S1=1,
,n∈N*,令n=1,则S2﹣2S1=1,
∴a2+1﹣2=1,解得a2=2.
(2)解:由nSn+1﹣(n+1)Sn= ![]() ,n∈N*,变形为:
,n∈N*,变形为: ![]() =
= ![]() ,
,
∴数列 ![]() 是等差数列,首项为1,公差为
是等差数列,首项为1,公差为 ![]() .
.
∴ ![]() =1+
=1+ ![]() =
= ![]() ,
,
∴Sn= ![]() ,
,
∴当n≥2时,Sn﹣1= ![]() ,
,
an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n,
=n,
∴an=n.
【解析】(1)令n=2可得a2的值;(2)对已知条件进行变形,可得数列 { ![]() } 是等差数列,进而可得数列 {
} 是等差数列,进而可得数列 { ![]() } 的通项公式,再利用Sn与an的关系可得数列{an}的通项公式.
} 的通项公式,再利用Sn与an的关系可得数列{an}的通项公式.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系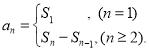 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案【题目】学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:
不关注 | 关注 | 总计 | |
男生 | 30 | 15 | 45 |
女生 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
根据表中数据,通过计算统计量K2= ![]() ,并参考一下临界数据:
,并参考一下临界数据:
P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
若由此认为“学生对2018年俄罗斯年世界杯的关注与性别有关”,则此结论出错的概率不超过( )
A.0.10
B.0.05
C.0.025
D.0.01