Question

【题目】已知函数 ；
（1）若函数 在 上为增函数，求正实数 的取值范围；
（2）当 时，求函数 在 上的最值；
（3）当 时，对大于1的任意正整数 ，试比较 与 的大小关系．

Answer 1

【答案】
（1）解：因为 ，所以

因为函数 在 上为增函数，所以 对 恒成立，

所以 对 恒成立，即 对 恒成立，所以

（2）解：当 时， ，所以当 时， ，故 在 上单调递减；当 ， ，故 在 上单调递增，所以 在区间 上有唯一极小值点，故 ，又 ， ，，

因为 ，所以 ，即

所以 在区间 上的最大值是

综上可知，函数 在区间 上的最大值是 ，最小值是0

（3）解：当 时， ， ，故 在 上为增函数.

当 时，令 ，则 ，故

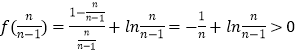所以 ，即 >

当a=1时，对大于1的任意正整数 ，有 >

【解析】(1)根据题意结合已知条件求出原函数的导函数利用导函数在指定区间上的正负情况得出原函数的增减性即可。(2)把a的值代入求出原函数的导函数并判断出其正负得到原函数的单调性，进而求出 f ( x ) 在区间 [ , 2 ) 上有唯一极小值点，代入数值求出结果即可得到最大值。(3)求出函数的导数得出函数的单调性，令x=得到 f ( x ) > f ( 1 ) = 0，从而证出结论。