题目内容
【题目】已知函数f(x)=|x﹣1|﹣|2x+1|的最大值为m
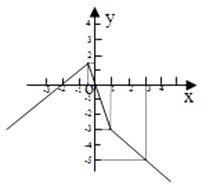
(1)作函数f(x)的图象
(2)若a2+b2+2c2=m,求ab+2bc的最大值.
【答案】
(1)解:f(x)=|x﹣1|﹣|2x+1|= 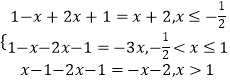 ,
,
由分段函数的图象画法可得图象如右
(2)解:由(1)知,当x=﹣ ![]() 时,f(x)的最大值为
时,f(x)的最大值为 ![]() ,即m=
,即m= ![]() ;
;
∴a2+b2+2c2= ![]() ,
,
设a2+b2+2c2=a2+tb2+(1﹣t)b2+2c2≥2 ![]() ab+2
ab+2 ![]() bc,
bc,
令2 ![]() :2
:2 ![]() =1:2,即8(1﹣t)=16t 得:t=
=1:2,即8(1﹣t)=16t 得:t= ![]() ,
,
∴a2+b2+2c2=a2+ ![]() b2+
b2+ ![]() b2+2c2≥2
b2+2c2≥2 ![]() ab+4
ab+4 ![]() bc=
bc= ![]() (ab+2bc)
(ab+2bc)
∴ab+2bc≤ ![]() (a2+b2+2c2)=
(a2+b2+2c2)= ![]() (当且仅当a2=c2=
(当且仅当a2=c2= ![]() ,b2=
,b2= ![]() 时取“=”号)
时取“=”号)
【解析】(1)讨论x的范围:x≤﹣ ![]() ,﹣
,﹣ ![]() <x≤1,x≥1,去掉绝对值,写出分段函数的形式,画出图象;(2)通过图象可得最大值m,设a2+b2+2c2=a2+tb2+(1﹣t)b2+2c2≥2
<x≤1,x≥1,去掉绝对值,写出分段函数的形式,画出图象;(2)通过图象可得最大值m,设a2+b2+2c2=a2+tb2+(1﹣t)b2+2c2≥2 ![]() ab+2
ab+2 ![]() bc,令2
bc,令2 ![]() :2
:2 ![]() =1:2,求出t的值,即可得到所求最大值.
=1:2,求出t的值,即可得到所求最大值.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目