题目内容
【题目】当![]() 时,函数
时,函数![]() 的值域是_________.
的值域是_________.
【答案】[-1,2]
【解析】:f(x)=sinx+![]() cosx=2(
cosx=2(![]() sinx+
sinx+![]() cosx)=2sin(x+
cosx)=2sin(x+![]() ),
),
∵﹣![]() ≤x≤
≤x≤![]() ,
,
∴﹣![]() ≤x+
≤x+![]() ≤
≤![]() ,
,
∴﹣![]() ≤sin(x+
≤sin(x+![]() )≤1,
)≤1,
∴函数f(x)的值域为[﹣1,2],
故答案为:[﹣1,2].
【题型】填空题
【结束】
15
【题目】若点O在![]() 内,且满足
内,且满足![]() ,设
,设![]() 为
为![]() 的面积,
的面积, ![]() 为
为![]() 的面积,则
的面积,则![]() =________.
=________.
【答案】![]()
【解析】由![]() ,可得:
,可得: ![]()
延长OA,OB,OC,使OD=2OA,OE=4OB,OF=3OC,
如图所示:
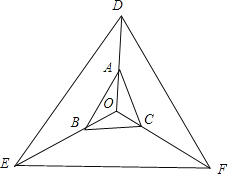
∵2![]() +3
+3![]() +4
+4![]() =
=![]() ,
,
∴![]() ,
,
即O是△DEF的重心,
故△DOE,△EOF,△DOF的面积相等,
不妨令它们的面积均为1,
则△AOB的面积为![]() ,△BOC的面积为
,△BOC的面积为![]() ,△AOC的面积为
,△AOC的面积为![]() ,
,
故三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() :
: ![]() :
: ![]() =3:2:4,
=3:2:4,
![]() .
.
故答案为: ![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目



