题目内容
(本题满分16分)
已知有穷数列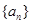 共有
共有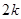 项(整数
项(整数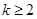 ),首项
),首项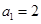 ,设该数列的前
,设该数列的前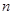 项和为
项和为 ,且
,且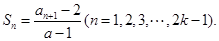 其中常数
其中常数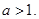 ⑴求
⑴求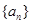 的通项公式;⑵若
的通项公式;⑵若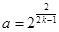 ,数列
,数列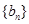 满足
满足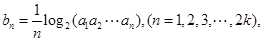
求证: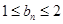 ;
;
⑶若⑵中数列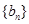 满足不等式:
满足不等式: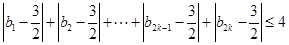 ,求
,求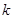 的最大值.
的最大值.
【答案】
⑴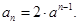 ⑵
⑵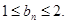 ⑶整数
⑶整数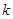 的最大值为7。
的最大值为7。
【解析】
试题分析:⑴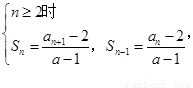
两式相减得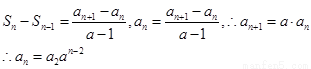
当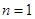 时
时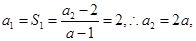 则,数列
则,数列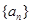 的通项公式为
的通项公式为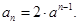
⑵把数列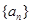 的通项公式代入数列
的通项公式代入数列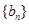 的通项公式,可得
的通项公式,可得
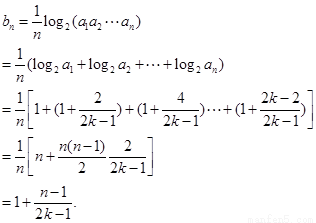
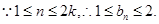
⑶数列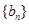 单调递增,且
单调递增,且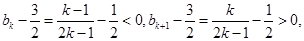
则原不等式左边即为
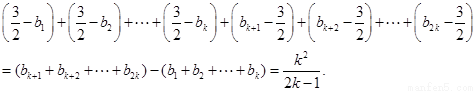
由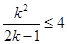 可得
可得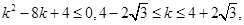 因此整数
因此整数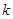 的最大值为7。
的最大值为7。
考点:本题主要考查数列的的基础知识,简单不等式的解法。
点评:中档题,本解答从研究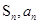 的关系入手,确定得到通项公式
的关系入手,确定得到通项公式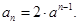 ,从而进一步明确
,从而进一步明确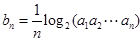 证明了
证明了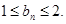 。“分组求和法”、“裂项相消法”、“错位相消法”是高考常常考到数列求和方法。
。“分组求和法”、“裂项相消法”、“错位相消法”是高考常常考到数列求和方法。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在