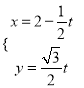题目内容
【题目】已知:全集U=R,函数 ![]() 的定义域为集合A,集合B={x|x2﹣a<0}
的定义域为集合A,集合B={x|x2﹣a<0}
(1)求UA;
(2)若A∪B=A,求实数a的范围.
【答案】
(1)解:∵ ![]() ,
,
∴﹣2<x<3,即A=(﹣2,3),
∵全集U=R,
∴CUA=(﹣∞,﹣2]∪[3,+∞);
(2)解:当a≤0时,B=,满足A∪B=A;
当a>0时,B=(﹣ ![]() ,
, ![]() ),
),
∵A∪B=A,∴BA,
∴ ![]() ,
,
∴0<a≤4,
综上所述:实数a的范围是a≤4
【解析】(1)求出f(x)的定义域,确定出A,由全集U=R,求出A的补集即可;(2)根据A与B的并集为A得到B为A的子集,分a小于等于0与a大于0两种情况考虑,即可确定出a的范围.
【考点精析】解答此题的关键在于理解集合的并集运算的相关知识,掌握并集的性质:(1)A![]() A∪B,B
A∪B,B![]() A∪B,A∪A=A,A∪
A∪B,A∪A=A,A∪![]() =A,A∪B=B∪A;(2)若A∪B=B,则A
=A,A∪B=B∪A;(2)若A∪B=B,则A![]() B,反之也成立,以及对集合的补集运算的理解,了解对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制.
B,反之也成立,以及对集合的补集运算的理解,了解对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目