题目内容
一边长为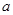 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积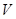 表示为
表示为 的函数;(2)
的函数;(2) 多大时,方盒的容积
多大时,方盒的容积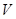 最大?
最大?
(1)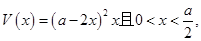 (2)当
(2)当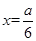 时,无盖方盒的容积
时,无盖方盒的容积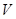 最大
最大
解析试题分析:由于在边长为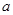 的正方形铁片的四角截去四个边长为
的正方形铁片的四角截去四个边长为 的小正方形,做成一个无盖方盒,
的小正方形,做成一个无盖方盒,
所以无盖方盒的底面是正方形,且边长为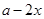 ,高为
,高为 , 2分
, 2分
(1)无盖方盒的容积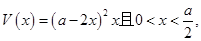 5分
5分
(2)因为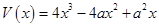 ,
,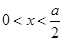 .
.
所以 ,令
,令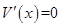 得
得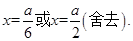 9分
9分
当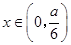 时,
时,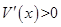 ;当
;当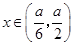 时,
时,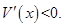 11分
11分
因此,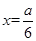 是函数
是函数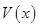 的极大值点,也是最大值点。 12分
的极大值点,也是最大值点。 12分
所以,当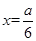 时,无盖方盒的容积
时,无盖方盒的容积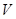 最大。 3分
最大。 3分
答:当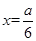 时,无盖方盒的容积
时,无盖方盒的容积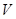 最大。 14分
最大。 14分
考点:本小题主要考查导数在实际问题中的应用.
点评:利用导数解决实际问题时,不要忘记函数本身的定义域,求最值时,要说清楚函数的单调性,步骤要完整.

练习册系列答案
相关题目
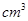 ,高为2
,高为2 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省? 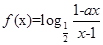 为奇函数,
为奇函数,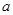 为常数,
为常数, 在区间
在区间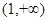 上单调递增;
上单调递增;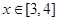 ,不等式
,不等式 恒成立,求实数
恒成立,求实数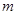 的取值范围。
的取值范围。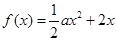 ,
,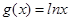 .
.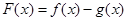 ,求函数
,求函数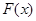 的单调区间;
的单调区间; 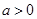 ,使得方程
,使得方程 在区间
在区间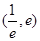 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
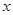 小时的收费为
小时的收费为 元
元 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动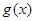 元
元