题目内容
【题目】利用一半径为4cm的圆形纸片(圆心为O)制作一个正四棱锥．方法如下：
(1)以O为圆心制作一个小的圆；
(2)在小的圆内制作一内接正方形ABCD；
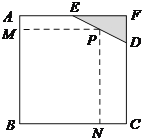
(3)以正方形ABCD的各边向外作等腰三角形，使等腰三角形的顶点落在大圆上(如图)；
(4)将正方形ABCD作为正四棱锥的底，四个等腰三角形作为正四棱锥的侧面折起，使四个等腰三角形的顶点重合，问：要使所制作的正四棱锥体积最大，则小圆的半径为
A. 
B. 
C. 
D. 
【答案】C
【解析】
设小圆的半径为
，连OD.OH.OH与AD交于点M，表示正四棱锥的体积
，利用导数研究函数的最值，即可得到结果.
设小圆的半径为，连OD.OH.OH与AD交于点M，则
.因为大圆半径R=4，所以
，在正四棱锥中，如图所示，
.
所以
记
，所以令
，
易知，
时，
取最大值，所以小圆半径为
时，V最大。故选C.
练习册系列答案
阅读快车系列答案
相关题目
