题目内容

10．在△ABC中，sinB+sinAcosC=0，求tanB的最大值．

分析 由条件可得A为锐角，再利用诱导公式、同角三角函数的基本关系求得tanC=-2tanA，再根据tanB=-tan（A+C）=$\frac{1}{tanA+\frac{1}{tanA}}$，利用基本不等式求得它的最大值．

解答 解：△ABC中，由sinB+sinAcosC=0，可得C为钝角，故A为锐角，故tanA＞0．
再根据sinB=sin[π-（A+C）]=sin（A+C）=sinAcosC+cosAsinC=-sinAcosC，
∴2sinAcosC=-cosAsinC，可得tanC=-2tanA，
∴tanB=-tan（A+C）=$\frac{tanA+tanC}{tanAtanC-1}$=$\frac{-tanA}{-{2tan}^{2}A-1}$=$\frac{tanA}{{tan}^{2}A+1}$=$\frac{1}{tanA+\frac{1}{tanA}}$≤$\frac{1}{2\sqrt{tanA•\frac{1}{tanA}}}$=$\frac{1}{2}$，
当且仅当tanA=1，即A=$\frac{π}{4}$时，tanB取得最大值为$\frac{1}{2}$．

点评 本题主要考查诱导公式、同角三角函数的基本关系、基本不等式的应用，属于基础题．

练习册系列答案
相关题目
20．已知f1（x）=sinx+cosx，且f2（x）=f1′（x），f3（x）=f2′（x），…，fn（x）=fn-1′（x），…（n∈N*，n≥2），则f1（$\frac{π}{4}$）+f2（$\frac{π}{4}$）+…+f2015（$\frac{π}{4}$）=0．
1．关于x的不等式x2-2x+3＞0解集为（　　）
A．（-1，3）B．∅C．RD．（-∞，-1）∪（3，+∞）
18．已知直线L1：（3+m）x+4y=5-3m与直线L2：2x+（6+m）y=8垂直，则m的值为（　　）
A．5B．-5C．3D．-4
5．已知数列{an}是以a为首项，q为公比的等比数列，Sn为它的前n项和．
（1）当S1，S3，S4成等差数列时，求q的值；
（2）若bn=anan+1（n∈N+），试求数列{bn}的前n项和Sn的公式．
15．已知|$\overrightarrow{a}$|=3，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，$\overrightarrow{c}$=$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{d}$=m$\overrightarrow{a}$-6$\overrightarrow{b}$（m∈R）．若$\overrightarrow{c}$∥$\overrightarrow{d}$，|$\overrightarrow{c}$+$\overrightarrow{d}$|=5$\sqrt{19}$．
2．设向量$\overrightarrow{a}$=（λ+2，λ2-$\sqrt{3}$cosα），$\overrightarrow{b}$=（m，$\frac{m+sinα}{2}$），其中λ，m，α为实数．
（1）若λ=m=0，$\overrightarrow{a}$•$\overrightarrow{b}$=cos2α+$\frac{1}{8}$，求tanα；
（2）若$\overrightarrow{a}$=2$\overrightarrow{b}$，求$\frac{λ}{m}$的取值范围．
19．计算：$\sqrt{3+2\sqrt{2}}$．
20．已知函数f（x）的部分图象如图，则f（x）的解析式可能为（　　）
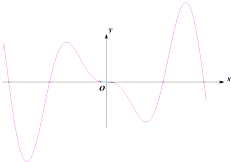
A．f（x）=xcosx-sinxB．f（x）=xsinxC．f（x）=xcosx+sinxD．f（x）=xcosx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网