题目内容
8.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,点B(0,b),过点B且与BF2垂直的直线交x轴负半轴于点D,且2$\overrightarrow{{F}_{1}{F}_{2}}$+$\overrightarrow{{F}_{2}D}$=$\overrightarrow{0}$.(1)求证:△BF1F2是等边三角形;
(2)若过B、D、F2三点的圆恰好与直线l:x-$\sqrt{3}$y-3=0相切,求椭圆C的方程;
(3)设过(2)中椭圆C的右焦点F2且不与坐标轴垂直的直线l与C交于P、Q两点,M是点P关于x轴的对称点.在x轴上是否存在一个定点N,使得M、Q、N三点共线,若存在,求出点N的坐标;若不存在,请说明理由.
分析 (1)设D(x0,0)(x0<0),利用$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{{F_2}D}=\vec 0$得b2=3c2,求解∠BF2F1=60°,证明△BF1F2是等边三角形.
(2)求出点D的坐标,利用△BDF2是直角三角形,得到其外接圆圆心为F1(-c,0),半径为2c,然后求解所求椭圆C的方程.
(3)直线l过F2且不与坐标轴垂直,设直线l的方程为:y=k(x-1),k≠0.与椭圆联立,设P(x1,y1),Q(x2,y2),结合韦达定理,求解直线QM的方向向量,求解直线QM的方程,求解直线QM与x轴交于定点(4,0).推出结果.
解答 (本题满分16分)本题共有3个小题,第1小题满分(4分),第2小题满分(6分),第3小题满分(6分).
解:(1)证明:设D(x0,0)(x0<0),由F2(c,0),B(0,b),故$\overrightarrow{{F_2}B}=(-c\;,\;b)$,$\overrightarrow{BD}=({x_0}\;,\;-b)$,
因为$\overrightarrow{{F_2}B}⊥\overrightarrow{BD}$,所以$-c{x_0}-{b^2}=0$,…(1分)
${x_0}=-\frac{b^2}{c}$,故$\overrightarrow{{F_2}D}=({-\frac{b^2}{c}-c\;,\;0})$,…(2分)
又$\overrightarrow{{F_1}{F_2}}=(2c\;,\;0)$,故由$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{{F_2}D}=\vec 0$得$3c-\frac{b^2}{c}=0$,所以,b2=3c2.…(3分)
所以,$tan∠B{F_2}{F_1}=\frac{b}{c}=\sqrt{3}$,∠BF2F1=60°,即△BF1F2是等边三角形.…(4分)
(2)由(1)知,$b=\sqrt{3}c$,故a=2c,此时,点D的坐标为(-3c,0),…(1分)
又△BDF2是直角三角形,故其外接圆圆心为F1(-c,0),半径为2c,…(3分)
所以,$\frac{|-c-3|}{2}=2c$,c=1,$b=\sqrt{3}$,a=2,…(5分)
所求椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$. …(6分)
(3)由(2)得F2(1,0),因为直线l过F2且不与坐标轴垂直,
故可设直线l的方程为:y=k(x-1),k≠0. …(1分)
由$\left\{\begin{array}{l}y=k(x-1)\;\\ \frac{x^2}{4}+\frac{y^2}{3}=1\;\end{array}\right.$得(3+4k2)x2-8k2x+4k2-12=0,…(2分)
设P(x1,y1),Q(x2,y2),则有${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$,${x_1}{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$,…(3分)
由题意,M(x1,-y1),故直线QM的方向向量为$\vec d=({x_2}-{x_1}\;,\;{y_2}+{y_1})$,
所以直线QM的方程为$\frac{{x-{x_1}}}{{{x_2}-{x_1}}}=\frac{{y+{y_1}}}{{{y_2}+{y_1}}}$,…(4分)
令y=0,得$x=\frac{{{y_1}({x_2}-{x_1})}}{{{y_2}+{y_1}}}+{x_1}=\frac{{{y_1}{x_2}+{y_2}{x_1}}}{{{y_2}+{y_1}}}=\frac{{k({x_1}-1){x_2}+k({x_2}-1){x_1}}}{{k({x_2}-1)+k({x_1}-1)}}$=$\frac{{2k{x_1}{x_2}-k({x_1}+{x_2})}}{{k({x_1}+{x_2})-2k}}$=$\frac{{2{x_1}{x_2}-({x_1}+{x_2})}}{{({x_1}+{x_2})-2}}$
=$\frac{{2•\frac{{4{k^2}-12}}{{3+4{k^2}}}-\frac{{8{k^2}}}{{3+4{k^2}}}}}{{\frac{{8{k^2}}}{{3+4{k^2}}}-2}}$=$\frac{-24}{-6}=4$.…(5分)
即直线QM与x轴交于定点(4,0).
所以,存在点N(4,0),使得M、Q、N三点共线. …(6分)
(注:若设N(x0,0),由M、Q、N三点共线,得$|{\begin{array}{l}{x_1}&{-{y_1}}&1\\{{x_2}}&{y_2}&1\\{{x_0}}&0&1\end{array}}|=0$,
得${x_0}=\frac{{{x_1}{y_2}+{x_2}{y_1}}}{{{y_1}+{y_2}}}$.)
点评 本题考查直线与椭圆的综合应用,椭圆的方程的求法,三点共线,考查分析问题解决问题的能力.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案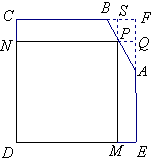 有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.
有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2. 