题目内容
19.若实数x,y满足$\left\{\begin{array}{l}x+2y≥2\\ x≤2\\ y≤1\end{array}\right.$,则x2+y2的最小值为$\frac{4}{5}$.分析 由题意画出图形,由点到直线的距离公式求得可行域内点与原点距离最小值的平方得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x+2y≥2\\ x≤2\\ y≤1\end{array}\right.$作出可行域如图,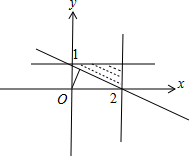
由图可知,x2+y2的最小值为坐标原点O到直线x+2y-2=0的距离的平方,
等于$(\frac{|-2|}{\sqrt{{1}^{2}+{2}^{2}}})^{2}=\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
10.执行如图的程序框图,若输入的a=209,b=76,则输出的a是( )


| A. | 3 | B. | 57 | C. | 19 | D. | 76 |
 如图,在四棱锥 A-BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4.
如图,在四棱锥 A-BCDE中,侧面△ADE为等边三角形,底面 BCDE是等腰梯形,且CD∥B E,DE=2,CD=4,∠CD E=60°,M为D E的中点,F为AC的中点,且AC=4.
 在三棱柱ABC-A1B1C1中,底面△ABC为正三角形,且${A_1}{B_1}=\frac{{\sqrt{3}}}{2}{A_1}A$,点A在下底面的射影是△A1B1C1的中心O.
在三棱柱ABC-A1B1C1中,底面△ABC为正三角形,且${A_1}{B_1}=\frac{{\sqrt{3}}}{2}{A_1}A$,点A在下底面的射影是△A1B1C1的中心O.