题目内容
3.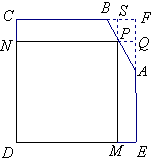 有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.
有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2. (1)试求出矩形铁皮DMPN的面积y关于x的函数解析式,并写出定义域;
(2)试问如何截取(即x取何值时),可使得到的矩形DMPN的面积最大?
分析 (1)依据题意并结合图形,可知:10当点P在线段CB上;20当点P在线段BA上,分别求解函数的解析式.(2)利用(1)知,当0<x≤30时,当30<x≤40时,分别求解函数的最大值即可.
解答 (本题满分14分)本题共有2个小题,第1小题满分(6分),第2小题满分(8分).
解(1)依据题意并结合图形,可知:10当点P在线段CB上,即0<x≤30时,y=40x;20当点P在线段BA上,即30<x≤40时,由$\frac{PQ}{QA}=\frac{BF}{FA}$,得$QA=48-\frac{6}{5}x$.
于是,$y=DM•PM=DM•EQ=76x-\frac{6}{5}{x^2}$.
所以,$y=\left\{\begin{array}{l}40x,0<x≤30\\ 76x-\frac{6}{5}{x^2}.30<x≤40\end{array}\right.$定义域D=(0,40].
(2)由(1)知,当0<x≤30时,0<y≤1200;
当30<x≤40时,$y=76x-\frac{6}{5}{x^2}=-\frac{6}{5}{(x-\frac{95}{3})^2}+\frac{3610}{3}≤\frac{3610}{3}$,当且仅当$x=\frac{95}{3}$时,等号成立.
因此,y的最大值为$\frac{3610}{3}$.
答:先在DE上截取线段$DM=\frac{95}{3}cm$,然后过点M作DE的垂线交BA于点P,再过点P作DE的平行线交DC于点N,最后沿MP与PN截铁皮,所得矩形面积最大,最大面积为$\frac{3610}{3}$cm2.
点评 本题考查函数的实际应用,函数的最值的求法,分段函数的解析式以及最值的求解,考查计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.绵阳市某高中的5名高三学生计划在高考结束后到北京、上海、杭州、广州等4个城市去旅游,要求每个城市都要有学生去,每个学生只去一个城市旅游,且学生甲不到北京,则不同的出行安排有( )
| A. | 180种 | B. | 72种 | C. | 216种 | D. | 204种 |
 在三棱柱ABC-A1B1C1中,底面△ABC为正三角形,且${A_1}{B_1}=\frac{{\sqrt{3}}}{2}{A_1}A$,点A在下底面的射影是△A1B1C1的中心O.
在三棱柱ABC-A1B1C1中,底面△ABC为正三角形,且${A_1}{B_1}=\frac{{\sqrt{3}}}{2}{A_1}A$,点A在下底面的射影是△A1B1C1的中心O.