题目内容
已知曲线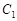 的极坐标方程为
的极坐标方程为 ,曲线
,曲线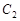 的极坐标方程为
的极坐标方程为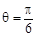 ,曲线
,曲线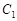 、
、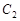 相交于
相交于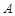 、
、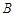 两点.(
两点.(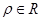 )
)
(Ⅰ)求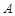 、
、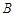 两点的极坐标;
两点的极坐标;
(Ⅱ)曲线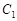 与直线
与直线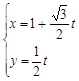 (
(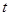 为参数)分别相交于
为参数)分别相交于 两点,求线段
两点,求线段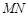 的长度.
的长度.
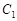 的极坐标方程为
的极坐标方程为 ,曲线
,曲线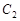 的极坐标方程为
的极坐标方程为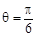 ,曲线
,曲线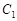 、
、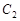 相交于
相交于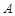 、
、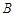 两点.(
两点.(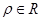 )
)(Ⅰ)求
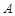 、
、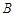 两点的极坐标;
两点的极坐标;(Ⅱ)曲线
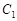 与直线
与直线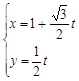 (
(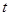 为参数)分别相交于
为参数)分别相交于 两点,求线段
两点,求线段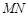 的长度.
的长度.(Ⅰ):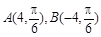 或
或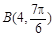 ;(Ⅱ)
;(Ⅱ)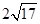 .
.
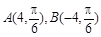 或
或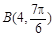 ;(Ⅱ)
;(Ⅱ)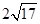 .
.试题分析:(Ⅰ)由
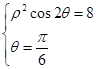 得:
得: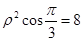 即可得到
即可得到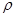 .进而得到点
.进而得到点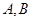 的极坐标.
的极坐标.(Ⅱ)由曲线
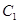 的极坐标方程
的极坐标方程 化为
化为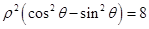 ,即可得到普通方程
,即可得到普通方程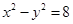 .将直线
.将直线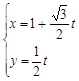 代入
代入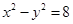 ,整理得
,整理得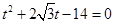 .进而得到
.进而得到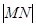 .
.试题解析:(Ⅰ)由
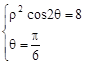 得:
得: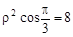
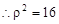 ,即
,即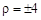 3分
3分所以
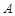 、
、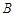 两点的极坐标为:
两点的极坐标为: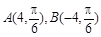 或
或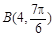 5分
5分(Ⅱ)由曲线
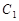 的极坐标方程得其普通方程为
的极坐标方程得其普通方程为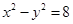 6分
6分将直线
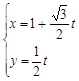 代入
代入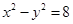 ,整理得
,整理得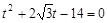 8分
8分所以
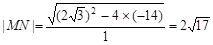

练习册系列答案
相关题目
 与椭圆
与椭圆 中心在原点,焦点均在
中心在原点,焦点均在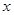 轴上,且离心率相同.椭圆
轴上,且离心率相同.椭圆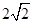 ,且椭圆
,且椭圆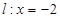 被椭圆
被椭圆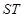 长为
长为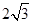 ,已知点
,已知点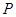 是椭圆
是椭圆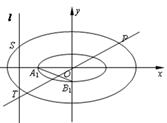
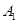 为椭圆
为椭圆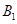 为椭圆
为椭圆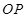 刚好平分
刚好平分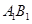 ,求点
,求点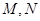 在椭圆
在椭圆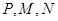 满足
满足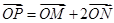 ,则直线
,则直线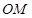 与直线
与直线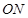 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.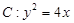 的焦点为
的焦点为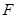 ,过点
,过点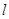 交抛物线
交抛物线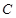 于点
于点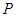 ,
,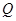 .
.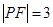 (点
(点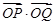 为定值(点
为定值(点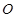 为坐标原点).
为坐标原点).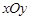 中,已知过点
中,已知过点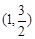 的椭圆
的椭圆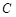 :
: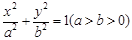 的右焦点为
的右焦点为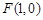 ,过焦点
,过焦点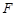 且与
且与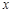 轴不重合的直线与椭圆
轴不重合的直线与椭圆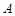 ,
,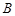 两点,点
两点,点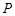 ,直线
,直线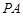 ,
,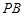 分别交椭圆
分别交椭圆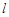 于
于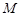 ,
,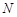 两点.
两点.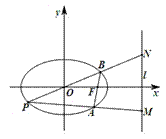
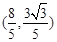 ,试求直线
,试求直线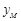 ,
,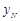 ,试问
,试问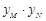 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由. 两焦点坐标分别为
两焦点坐标分别为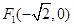 ,
,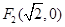 ,一个顶点为
,一个顶点为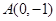 .
.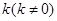 的直线
的直线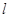 ,使直线
,使直线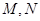 ,满足
,满足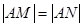 . 若存在,求出
. 若存在,求出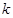 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.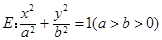 与双曲线
与双曲线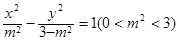 有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线
有公共的焦点,过椭圆E的右顶点作任意直线l,设直线l交抛物线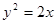 于M、N两点,且
于M、N两点,且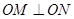 .
.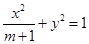 的两个焦点是F1(
的两个焦点是F1(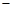 c,0),F2(c,0)(c>0)。
c,0),F2(c,0)(c>0)。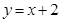 与椭圆C有公共点,求
与椭圆C有公共点,求 的取值范围;
的取值范围;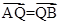 且
且 ,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.
,其中N为椭圆的下顶点,求直线l在y轴上截距的取值范围.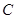 的中心在原点,焦点在
的中心在原点,焦点在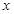 轴上,长轴长为
轴上,长轴长为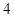 ,且点
,且点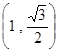 在椭圆
在椭圆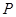 是椭圆
是椭圆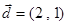 的直线
的直线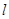 交椭圆
交椭圆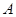 、
、 两点,求证:
两点,求证: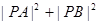 为定值.
为定值.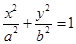
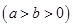 的左、右焦点分别是
的左、右焦点分别是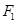 、
、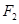 ,
,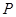 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段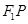 的垂直平分线过点
的垂直平分线过点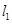 :
: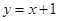 按向量
按向量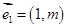 平移后的直线是
平移后的直线是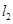 ,直线
,直线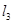 :
: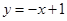 按向量
按向量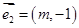 平移后的直线是
平移后的直线是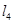 (其中
(其中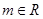 )。
)。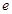 的取值范围。
的取值范围。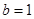 时,求椭圆的方程。
时,求椭圆的方程。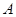 、
、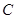 两点,
两点,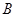 、
、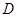 两点。求四边形ABCD面积
两点。求四边形ABCD面积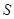 的取值范围。
的取值范围。