题目内容
【题目】椭圆
的长轴是短轴的两倍，点
在椭圆上.不过原点的直线
与椭圆相交于
、
两点，设直线
、、
的斜率分别为
、
、
，且、、恰好构成等比数列，
（1）求椭圆
的方程；
（2）试判断
是否为定值？若是，求出这个值；若不是，请说明理由？
【答案】（1）
（2）是，
是定值为5；
【解析】
（1）由题得方程组：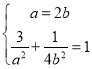
解得
，即可得椭圆方程；
（2）联立
，消元得：
；由
、
、
且恰好构成等比数列，得到：
，代入求得：
，最后算出
，代入化简即可得结果.
解：（1）由题意可知
，且
，
所以椭圆的方程为
（2）依题意，直线
斜率存在且
，设直线的方程为
，
、
由
因为、、且恰好构成等比数列，
所以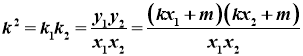
，
即
；
所以
.
此时
得
，且
（否则：
，则
，
中至少有一个为0，一直线
、
中至少有一个斜率不存在，与已知矛盾）
所以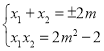
；
所以
所以是定值为5；
练习册系列答案
相关题目
【题目】一个工厂在某年里连续10个月每月产品的总成本
（万元）与该月产量
（万件）之间有如下一组数据：
| 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
| 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
（1）通过画散点图，发现可用线性回归模型拟合与的关系，请用相关系数
加以说明；
（2）①建立月总成本与月产量之间的回归方程；②通过建立的关于的回归方程，估计某月产量为1.98万件时，产品的总成本为多少万元？（均精确到0.001）
附注：①参考数据：
，
，
，
，
.
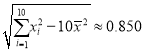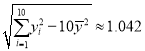②参考公式：相关系数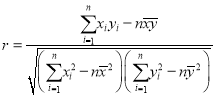
，
，
.
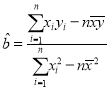