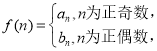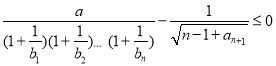题目内容
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,长轴长为
,长轴长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程及离心率;
的标准方程及离心率;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,求证:由点
,求证:由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.
【答案】(Ⅰ)![]() ,离心率
,离心率![]() ;(Ⅱ)见解析
;(Ⅱ)见解析
【解析】
(Ⅰ)由已知,得a![]() ,c=1,所以
,c=1,所以![]() ,由
,由![]() ,所以b
,所以b![]() ,即可求出椭圆方程及离心率;(Ⅱ)设A(x1,y1),B(x2,y2),
,即可求出椭圆方程及离心率;(Ⅱ)设A(x1,y1),B(x2,y2),![]() ,分两种情况,借助韦达定理和向量的运算,求出点M构成的曲线L的方程为2x2+3y2﹣2y=0,即可证明。
,分两种情况,借助韦达定理和向量的运算,求出点M构成的曲线L的方程为2x2+3y2﹣2y=0,即可证明。
(Ⅰ)由已知,得![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]()
所以椭圆![]() 的标准方程为
的标准方程为![]() ,离心率
,离心率![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,
,
①直线![]() 与
与![]() 轴垂直时,点
轴垂直时,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以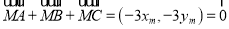 .
.
所以![]() ,即点
,即点![]() 与原点重合;
与原点重合;
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
由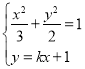
得![]() ,
,![]() .
.
所以![]() .
.
则![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,![]() .
.![]() ,
,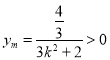 ,
,
消去![]() 得
得![]() .
.
综上,点![]() 构成的曲线
构成的曲线![]() 的方程为
的方程为![]()
对于曲线![]() 的任意一点
的任意一点![]() ,它关于直线
,它关于直线![]() 的对称点为
的对称点为![]() .
.
把![]() 的坐标代入曲线
的坐标代入曲线![]() 的方程的左端:
的方程的左端: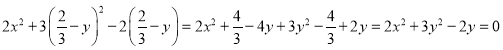 .
.
所以点![]() 也在曲线
也在曲线![]() 上.
上.
所以由点![]() 构成的曲线
构成的曲线![]() 关于直线
关于直线![]() 对称.
对称.

练习册系列答案
相关题目