��Ŀ����
����Ŀ����һ�ο�����,5��ͬѧ����ѧ�������ɼ������ʾ��
ѧ�� | A | B | C | D | E |
��ѧ(x��) | 89 | 91 | 93 | 95 | 97 |
����(y��) | 87 | 89 | 89 | 92 | 93 |
(1)���ݱ������ݣ���������y������ѧ��x�Ļع鷽�̣����Թ���ijͬѧ��ѧ��100��ʱ�����������÷֣�
(2)Ҫ��4����ѧ�ɼ���90�����ϵ�ͬѧ��ѡ��2���μ�һ������X��ʾѡ�е�ͬѧ�������ɼ�����90�ֵ��������Խ���������⣺
��������ѡ��1�������ɼ���90�����µ�ͬѧ�ĸ��ʣ�
������������X�ķֲ��м���ѧ����![]() ��
��
�����ع鷽�̣�![]() ��
��
���𰸡���1��![]() ��95.25����2����
��95.25����2����![]() ��E(X)=1
��E(X)=1
��������
��1�����ݱ��������ݼ�ƽ������ʽ�����![]() ��
��![]() ��ֵ���Ӷ��ɵ��������ĵ�����꣬������ɵù�ʽ
��ֵ���Ӷ��ɵ��������ĵ�����꣬������ɵù�ʽ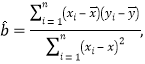 ���������ݣ����
���������ݣ����![]() ���ٽ���������ĵ�����ʿɵ�
���ٽ���������ĵ�����ʿɵ�![]() �������ɵ�
�������ɵ�![]() ����
����![]() �Ļع鷽������2��
�Ļع鷽������2��![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ��������֪ʶ�����ùŵ�����ʹ�ʽ����������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�
��������֪ʶ�����ùŵ�����ʹ�ʽ����������������Ӧ�ĸ��ʣ��Ӷ��ɵ÷ֲ��У���������������ʽ�ɵ�![]() ����ѧ����.
����ѧ����.
��1��![]() ��
��![]() ��
��
![]() ��
��
![]() =
=![]() ��
��
��![]() ��
��![]() 90��0.75��93=20.25��
90��0.75��93=20.25��
��������y������ѧ��x�Ļع鷽��Ϊ![]() ��
��
��x=100ʱ��![]() =0.75��100+20.25=95.25�֣�
=0.75��100+20.25=95.25�֣�
��2���������X�����п���ȡֵΪ0��1��2��
P(X=0)= ![]() =
=![]() ��P(X=1)=
��P(X=1)= ![]() =
=![]() ��P(X=2)=
��P(X=2)=![]() =
=![]() ��
��
������ѡ��1�������ɼ���90�����µ�ͬѧ�ĸ���ΪP=P(X=0)+P(X=1)=![]() ��
��
X | 0 | 1 | 2 |
P |
|
|
|
��X�ķֲ���Ϊ��
��X����ѧ����E(X)=0��![]() +1��
+1��![]() +2��
+2��![]() =1��
=1��
�������⣺дX���ӳ����ηֲַ�����X ~H��4��2��2����E(X)= 2��![]() =1����
=1����

����Ŀ��ij���չ�˾���һ��ӵ��20000�˵���ҵ�Ƴ�һ�������ղ�Ʒ��ÿ��ÿλְ��ֻҪ���������ѣ�����������һ���Ի�������⳥�𣮱��չ�˾����ҵ�����и�λ����ΪA��B��C����֣���������ֵ������ֲ�������ͼ��������ʷ����ͳ�Ƴ�����ֵ��⸶Ƶ�����±������Դ˹����⸶Ƶ�ʣ���
������� | A | B | C |
�⸶Ƶ�� |
|
|
|
����A��B��C�����ְ��ÿ��ÿ�걣�ѷֱ�ΪaԪ��aԪ��bԪ�����պ���⳥���ֱ�Ϊ100��Ԫ��100��Ԫ��50��Ԫ�����չ�˾�ڿ�չ����ҵ������еĹ̶�֧��Ϊÿ��10��Ԫ��
���������չ�˾Ҫ����������������ڱ��ѵ�20%����ȷ������a��b��Ҫ�����������
������������������������ҵѡ��
����1����ҵ���뱣�չ�˾��������ҵ�����ó��뱣���ṩ�ĵȶ���⳥����⸶������ְ����
����2����ҵ�뱣�չ�˾��������ҵ����ְ�����ѵ�60%��ְ�����˸��𱣷ѵ�40%�����պ��⳥���ɱ��չ�˾�⸶��
����ҵѡ��2��֧����������ְ��֧��������ѡ��1��֧����������a��b��Ҫ��������������ж���ҵ�Ƿ���뱣�չ�˾������������ҵѡ��2��֧������ѡ��1��֧�����������루���б��չ�˾����������ì�ܣ�����ҵ���뱣�չ�˾��������


