题目内容
【题目】已知椭圆 ![]() ,过
,过 ![]() 的直线l与椭圆交于A,B两点,过Q(x0 , 0)(|x0|<a)的直线l'与椭圆交于M,N两点.
的直线l与椭圆交于A,B两点,过Q(x0 , 0)(|x0|<a)的直线l'与椭圆交于M,N两点. 
(1)当l的斜率是k时,用a,b,k表示出|PA||PB|的值;
(2)若直线l,l'的倾斜角互补,是否存在实数x0 , 使 ![]() 为定值,若存在,求出该定值及x0 , 若不存在,说明理由.
为定值,若存在,求出该定值及x0 , 若不存在,说明理由.
【答案】
(1)解:椭圆 ![]() ,焦点在x轴上,焦距为2c,
,焦点在x轴上,焦距为2c,
设直线AB的方程: ![]() ,
,
由 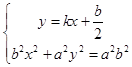 ,整理得:
,整理得: ![]() ,
,
由韦达定理可知: ![]() ,
,
![]()
(2)解:当直线MN的斜率存在时:设直线MN的方程:y=﹣k(x﹣x0),M(x3,y3),N(x4,y4).
由 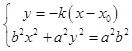 ,可知得:
,可知得: ![]() ,
,
则 ![]() ,
,
由韦达定理可知: ![]() ,
,
由弦长公式可知:丨MN丨= ![]()
![]() ,
,
∴ ![]() ,
,
![]() ,
,
∴当x0=0时, ![]() 为常数
为常数
当直线MN的斜率不存在时: 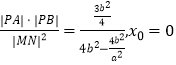 时,
时,
![]() 为定值.
为定值.
综上:所以当x0=0时, ![]() 为常数
为常数
【解析】(1)由题意可知:椭圆的焦点在x轴上,设直线AB的方程: ![]() ,代入椭圆方程,由韦达定理
,代入椭圆方程,由韦达定理 ![]() ,因此,由弦长公式可知:
,因此,由弦长公式可知: ![]() ,(2)当直线MN的斜率存在时:设直线MN的方程:y=﹣k(x﹣x0),代入椭圆方程,由韦达定理可知:
,(2)当直线MN的斜率存在时:设直线MN的方程:y=﹣k(x﹣x0),代入椭圆方程,由韦达定理可知: ![]() ,由弦长公式求得丨MN丨,则
,由弦长公式求得丨MN丨,则 ![]() ,
, ![]() ,当x0=0时,
,当x0=0时, ![]() 为常数,当直线MN的斜率不存在时:
为常数,当直线MN的斜率不存在时: 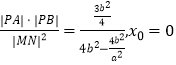 时,
时, ![]() 为定值,所以当x0=0时,
为定值,所以当x0=0时, ![]() 为常数.
为常数.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】在一次考试中,5名同学的数学、物理成绩如表所示:
学生 | A | B | C | D | E |
数学(x分) | 89 | 91 | 93 | 95 | 97 |
物理(y分) | 87 | 89 | 89 | 92 | 93 |
(1)根据表中数据,求物理分y关于数学分x的回归方程,并试估计某同学数学考100分时,他的物理得分;
(2)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,试解决下列问题:
①求至少选中1名物理成绩在90分以下的同学的概率;
②求随机变变量X的分布列及数学期望![]() .
.
附:回归方程:![]() 中
中

