题目内容
已知函数f(x)=ax·lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
答案:
解析:
解析:
|
解:(1)依题意有 ∵(e,f(e))在f(x)上;∴f(e)=aelne+b=ae+b=e,∴b=0 故实数 (2) (3) 由(2)知 故实数 |

练习册系列答案
相关题目
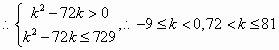 11分
11分 (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4. .
. (a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值.
(a,b为常数,且a≠0),满足f(2)=1,方程f(x)=x有唯一实数解,求函数f(x)的解析式和f[f(-4)]的值. )
)