题目内容
.(本小题满分14分)
已知一几何体的三视图如图(甲)示,(三视图中已经给出各投影面顶点的标记)
(1)在已给出的一个面上(图乙),
画出该几何体的直观图
(2)设点F、H、G分别为AC、AD、
DE的中点,求证:FG//平 面ABE;
面ABE;
(3)求该几何体的体积.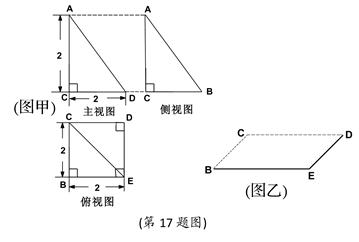
解:(1)该几何体的直观图如图示: ………………………… 4分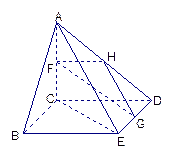
(说明:画 出AC
出AC 平面ABCD得2分,其余2分,其他
平面ABCD得2分,其余2分,其他
画法可按实际酌情给分)
(2)证法一:取BA的中点I,连接FI、IE,
∵F、I分别为AC、AB的中点,∴FI BC,………… 5分
BC,………… 5分
∵BC//ED ∴FI ED,
ED,
又EG= ED ,∴FI
ED ,∴FI EG
EG
∴四边形EGFI为平行四边形,……………………………………………………… 7分
∴EI//FG
又∵ 面
面 ,
, 面
面 ∴FG//平面ABE …………………………… 9分
∴FG//平面ABE …………………………… 9分
证法二:由图(甲)知四边形CBED为正方形
∵F、H、G分别为AC,AD ,DE的中点
∴FH//CD, HG//AE …………………………………………………………… 5分
∵CD//BE, ∴FH//BE
∵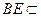 面
面 ,
, 面
面
∴ 面
面 …………………………………………………………………… 7分
…………………………………………………………………… 7分
同理可得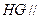 面
面
又∵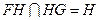 ∴平面FHG//平面ABE …………………………………… 8分
∴平面FHG//平面ABE …………………………………… 8分
又∵ 面
面 ∴FG//平面ABE ………………………………………… 9分
∴FG//平面ABE ………………………………………… 9分
(3)由图甲知AC CD,AC
CD,AC BC,
BC,
∴AC 平面ABCD, 即AC为四棱棱锥的高
平面ABCD, 即AC为四棱棱锥的高 …………………………… 10分
…………………………… 10分
∵底面ABCD是一个正方形, ……………………………………… 12分
……………………………………… 12分
∴该几何体的体积:  …………………………………………… 14分[
…………………………………………… 14分[
解析

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)