题目内容
【题目】已知椭圆 ![]() 为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为
为参数),A,B是C上的动点,且满足OA⊥OB(O为坐标原点),以原点O为极点,x轴的正半轴为极轴建立坐标系,点D的极坐标为 ![]() .
.
(1)求线段AD的中点M的轨迹E的普通方程;
(2)利用椭圆C的极坐标方程证明 ![]() 为定值,并求△AOB的面积的最大值.
为定值,并求△AOB的面积的最大值.
【答案】
(1)解:点D的直角坐标为 ![]() ,由题意可设点A的坐标为(2cosα,sinα)参数,
,由题意可设点A的坐标为(2cosα,sinα)参数,
则线段AD的中点M的坐标为 ![]() ,
,
所以点M的轨迹E的参数方程为 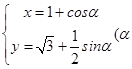 为参数)
为参数)
消去α可得E的普通方程为 ![]() .
.
(2)解:椭圆C的普通方程为 ![]() ,化为极坐标方程得ρ2+3ρ2sin2θ=4,
,化为极坐标方程得ρ2+3ρ2sin2θ=4,
变形得 ![]() ,
,
由OA⊥OB,不妨设 ![]() ,所以
,所以 ![]()
= 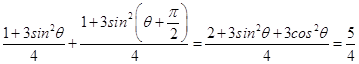 (定值),
(定值),
S△AOB= ![]() ρ1ρ2=
ρ1ρ2=  =
= 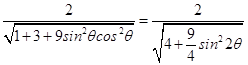 ,
,
易知当sin2θ=0时,S取得最大值1.
【解析】(1)由题意求得线段AD中点坐标M,即可求得M的轨迹E的参数方程,消去α,即可求得E的普通方程;(2)由椭圆的普通方程,求得极坐标方程,求得 ![]() ,由OA⊥OB,根据
,由OA⊥OB,根据 ![]() ,化简即可求得
,化简即可求得 ![]() =
= ![]() 为定值,根据三角形的面积公式,利用二倍角公式,及三角函数的性质,即可求得△AOB面积的最大值.
为定值,根据三角形的面积公式,利用二倍角公式,及三角函数的性质,即可求得△AOB面积的最大值.

练习册系列答案
相关题目