Question

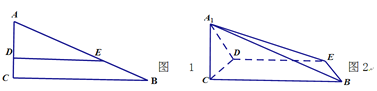
【题目】如图1，在Rt△ABC中，∠C=90°，BC=6，AC=3，D，E分别是AC，AB上的点，且DE∥BC，DE=4，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．

（1）求证：平面；

（2）过点E作截面 平面，分别交CB于F，于H，求截面的面积。

Answer 1

【答案】（1）详见解析（2）

【解析】试题分析：（1）证明DE⊥平面，可得⊥DE，利用⊥CD，CD∩DE=D，即可证明⊥平面BCDE；

（2）过点E作EF∥CD交BC于F，过点F作FH∥交A1B于H，连结EH，则截面EFH∥平面，从而可求截面EFH的面积

试题解析：（1） ， 平面．

又 平面， ．又， 平面

（2）过点E作EF∥CD交BC于F，过点F作FH∥

交于H，连结EH．则截面平面。因为四边形EFCD为矩形，

所以EF=CD=1，CF=DE=4，从而FB=2，HF= 平面，

FH∥，平面，