题目内容
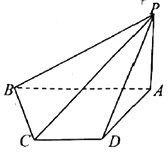
【题目】如图,在四棱柱![]() 中,侧面
中,侧面![]() ⊥底面
⊥底面![]() ,
,![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]()
![]() ,O为
,O为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]()
【解析】
(I)证明![]() ,即证:四边形AB1CO为平行四边形.
,即证:四边形AB1CO为平行四边形.
(II)![]() 为
为![]() 的中点,
的中点,![]() ,又侧面
,又侧面![]() ⊥底面
⊥底面![]() ,故
,故![]() ⊥底面
⊥底面![]() ,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
,然后建立直角坐标系,利用向量法求二面角,先求二面角两个面的法向量,然后再求法向量的夹角,根据法向量的夹角与二面角相等或互补来解.
(Ⅰ)证明:如图,连接![]() ,
,
则四边形![]() 为正方形,
为正方形,
![]() ,且
,且![]()
故四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(Ⅱ)![]() 为
为![]() 的中点,
的中点,![]() ,又侧面
,又侧面![]() ⊥底面
⊥底面![]() ,故
,故![]() ⊥底面
⊥底面![]() ,
,

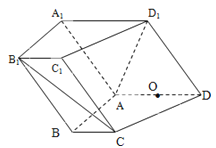
以![]() 为原点,所
为原点,所![]() 在直线分别为
在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则![]()
![]() ,
,
![]()
![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]()
又设![]() 为平面
为平面![]() 的一个法向量,由
的一个法向量,由![]() ,得
,得![]() ,令
,令
![]() ,则
,则![]() ,
,
则![]() ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为![]()
注:第2问用几何法做的酌情给分.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】已知z,y之间的一组数据如下表:
x | 1 | 3 | 6 | 7 | 8 |
y | 1 | 2 | 3 | 4 | 5 |
(1)从x ,y中各取一个数,求x+y≥10的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为![]() 与
与![]() ,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)”判断哪条直线拟合程度更好.