题目内容
过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是( )
| A.(x-3)2+(y+1)2=4 | B.(x+3)2+(y-1)2=4 |
| C.(x-1)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |
C
解析试题分析:由圆的几何性质,圆心一定在AB的中垂线y=x上,因此,排除A,B选项;
圆心在直线x+y-2=0上验证D选项,可知不成立.
故选C.
考点:圆的几何性质,圆的方程。
点评:简单题,本题灵活利用圆的几何性质即“排除法”,方便解答。

练习册系列答案
相关题目
过点 作圆
作圆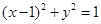 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,则直线
,则直线 的方程为( )
的方程为( )
A. | B. | C. | D.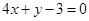 |
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为( )
的最小值为( )
A. | B. | C. | D.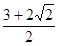 |
由直线 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )
A. | B. | C. | D. |
与直线 和圆
和圆 都相切的半径最小的圆的方程是( )
都相切的半径最小的圆的方程是( )
A. | B. |
C. | D. |
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
圆 :
: 与圆
与圆 :
: 的位置关系( )
的位置关系( )
| A.相交 | B.外切 | C.内切 | D.外离 |
 表示一个圆,则
表示一个圆,则 的取值范围是( )
的取值范围是( )
A. ≤2 ≤2 | B. | C. | D. ≤ ≤ |
若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2 ,则实数a的值为
,则实数a的值为
A.-1或 | B.1或3 | C.-2或6 | D.0或4 |