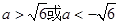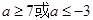若直线与圆相切.则的值为( )A． B． C． D．或题目和参考答案——青夏教育精英家教网—

题目内容

若直线与圆相切，则的值为（）

A．

B．

C．

D．

或

解析试题分析：根据题意，由于直线与圆相切，在圆心到直线的距离等于圆的半径，即可知，则可知的值为2，故可知答案为C
考点：直线与圆
点评：主要是考查直线与圆的位置关系的运用，属于基础题。

练习册系列答案

相关题目

已知点，,，以线段为直径作圆，则直线与圆的位置关系是（）

两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线，和圆相切，则的取值范围是（）

圆截直线所得弦长是（）

过点A（1，-1）、B（-1，1）且圆心在直线x+y-2=0上的圆的方程是（）

A．(x-3)²+(y+1)²=4	B．(x+3)²+(y-1)²=4
C．(x-1)²+(y-1)²=4	D．(x+1)²+(y+1)²=4

若直线与圆有公共点，则实数a取值范围是（）

A．[－3，－1]	B．[－1，3]
C．[－3,l ]	D．（－∞，－3] [1．+∞）

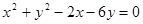在圆内，过点的最长弦和最短弦分别是AC和BD，则四边形ABCD的面积为

直线与圆相交于，两点，且,则的取值范围是（）

A．	B．
C．	D．

若函数的图象在处的切线与圆相离,则点与圆C的位置关系是 ( )

试题分类