题目内容
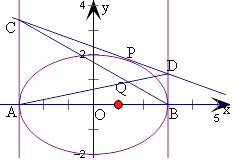
【题目】已知椭圆 
+ 
=1与x轴交于A、B两点，过椭圆上一点P（x0 ， y0）（P不与A、B重合）的切线l的方程为 
+ 
=1，过点A、B且垂直于x轴的垂线分别与l交于C、D两点，设CB、AD交于点Q，则点Q的轨迹方程为 ．
【答案】
+y2=1（x≠±3）
【解析】解：椭圆 
+ 
=1的a=3，
可得A（﹣3，0），B（3，0），
由x=﹣3代入切线l的方程为 
+ 
=1，
可得y= 
，即C（﹣3， ），
由x=3代入切线l的方程为 + =1，
可得y= 
，即D（3， ），
可得直线CB的方程为y= 
（x﹣3）①
直线AD的方程为y= 
（x+3）②
①×②可得y2=﹣ 
（x2﹣9），③
结合P在椭圆上，可得 
+ 
=1，
即有9﹣x02= 
，
代入③可得， +y2=1（x≠±3）．
所以答案是： +y2=1（x≠±3）．
练习册系列答案
相关题目
