题目内容
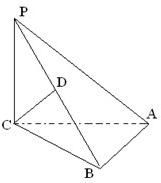 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.(1)求证:AB⊥平面PCB;
(2)求平面PAC和平面PAB所成锐二面角的余弦值.
分析:(1)根据PC⊥平面ABC,AB?平面ABC,则PC⊥AB,而CD⊥平面PAB,AB?平面PAB,则CD⊥AB,又PC∩CD=C,根据线面垂直的判断定理可知AB⊥平面PCB.
(2)取AP的中点E,连接CE、DE,PC=AC=2,则CE⊥PA,CE=
,因CD⊥平面PAB,由三垂线定理的逆定理,得DE⊥PA,从而∠CED为二面角C-PA-B的平面角.由(1)可知AB⊥平面PCB,又AB=BC,可得BC=
.在Rt△PCB中,求出PB,CD,在Rt△CDE中,求出∠CED的余弦值即可.
(2)取AP的中点E,连接CE、DE,PC=AC=2,则CE⊥PA,CE=
| 2 |
| 2 |
解答: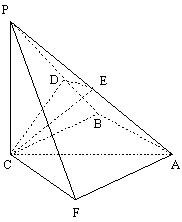 解(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.
解(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.
∵CD⊥平面PAB,AB?平面PAB,∴CD⊥AB.
又PC∩CD=C,∴AB⊥平面PCB.
(2)取AP的中点E,连接CE、DE.
∵PC=AC=2,∴CE⊥PA,CE=
.
∵CD⊥平面PAB,
由三垂线定理的逆定理,得DE⊥PA.
∴∠CED为二面角C-PA-B的平面角.
由(1)AB⊥平面PCB,又∵AB=BC,可得BC=
.
在Rt△PCB中,PB=
=
,
CD=
=
=
.
在Rt△CDE中,
sin∠CED=
=
=
.
∴cos∠CED=
 解(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.
解(1)∵PC⊥平面ABC,AB?平面ABC,∴PC⊥AB.∵CD⊥平面PAB,AB?平面PAB,∴CD⊥AB.
又PC∩CD=C,∴AB⊥平面PCB.
(2)取AP的中点E,连接CE、DE.
∵PC=AC=2,∴CE⊥PA,CE=
| 2 |
∵CD⊥平面PAB,
由三垂线定理的逆定理,得DE⊥PA.
∴∠CED为二面角C-PA-B的平面角.
由(1)AB⊥平面PCB,又∵AB=BC,可得BC=
| 2 |
在Rt△PCB中,PB=
| PC2+BC2 |
| 6 |
CD=
| PC•BC |
| PB |
2×
| ||
|
| 2 | ||
|
在Rt△CDE中,
sin∠CED=
| CD |
| CE |
| ||||
|
| ||
| 3 |
∴cos∠CED=
| ||
| 3 |
点评:本题主要考查了直线与平面垂直的判定,以及求二面角的问题,考查空间想象能力,几何逻辑推理能力,以及计算能力,属于中档题.

练习册系列答案
相关题目
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中, (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,