题目内容
【题目】记![]() 表示
表示![]() 中的最大值,如
中的最大值,如![]() ,已知函数
,已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的值域;
上的值域;
(2)试探讨是否存在实数![]() , 使得
, 使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;
的取值范围;
若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据题意,明确给定范围上的![]() 的表达式,然后求值域;(2)根据题意,明确给定范围上的
的表达式,然后求值域;(2)根据题意,明确给定范围上的![]() 的表达式,然后恒成立问题就转化为最值问题.
的表达式,然后恒成立问题就转化为最值问题.
试题解析:(1)设![]() ,.............1分
,.............1分
令![]() ,得
,得![]() 递增;令
递增;令![]() ,得
,得![]() 递减,.................2分
递减,.................2分
∴![]() ,∴
,∴![]() ,.......................3分
,.......................3分
即![]() ,∴
,∴![]() .............4分
.............4分
故函数![]() 在
在![]() 上的值域为
上的值域为![]() ...........................5分
...........................5分
(2)①当![]() 时,
时,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() .................................................. 6分
.................................................. 6分
若![]() ,对
,对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,
恒成立,
设![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() 递增;令
递增;令![]() ,得
,得![]() 递减.
递减.
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ....9分
....9分
②当![]() 时,由(1)知
时,由(1)知![]() ,对
,对![]() 恒成立,
恒成立,
若![]() 对
对![]() 恒成立,则
恒成立,则![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,这显然不可能.
恒成立,这显然不可能.
即当![]() 时,不满足
时,不满足![]() 对
对![]() 恒成立,.........................11分
恒成立,.........................11分
故存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,且
恒成立,且![]() 的取值范围为
的取值范围为![]() .......12分
.......12分

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 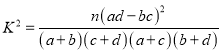 ,其中
,其中![]() )
)