题目内容
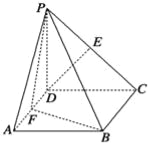
【题目】如图,平面![]() 平面
平面![]() ,其中
,其中![]() 为矩形,
为矩形,![]() 为直角三角形,
为直角三角形,![]() ,
,![]() .
.
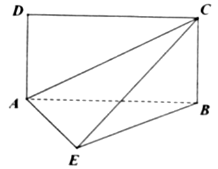
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)运用线面垂直的判定定理及面面垂直的判定定理推证;(2)运用线面角的定义运用解直角三角形的方法求解或建立空间直角坐标系,运用空间向量的数量积求解.
试题解析:
(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]()
![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]()
又![]() ,
,![]()
∴![]() 平面
平面![]()
而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
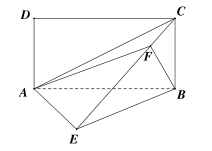
(2)解法一:
∵![]()
∴![]() 与平面
与平面![]() 所成角的大小等于
所成角的大小等于![]() 与平面
与平面![]() 所成角的大小
所成角的大小
过![]() 作
作![]() 于
于![]() ,连接
,连接![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]() 即为
即为![]() 与平面
与平面![]() 所成的角
所成的角
由![]() ,得
,得![]() ,
,![]()
∴![]()
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
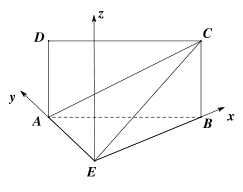
解法二:以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
则![]()
于是,![]() ,
,![]() ,
,![]()
设![]() 为平面
为平面![]() 的法向量
的法向量
由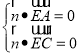 得
得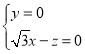
取![]()
设![]() 与
与![]() 的夹角为
的夹角为![]()
所以![]()
所以![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
相关题目