[题目]四棱锥P﹣ABCD中.四边形ABCD为正方形.PD⊥平面ABCD.PD=DA=2.F.E分别为AD.PC的中点．(1)证明:DE∥平面PFB,(2)求三棱锥A﹣PFB的体积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】四棱锥P﹣ABCD中，四边形ABCD为正方形，PD⊥平面ABCD，PD=DA=2，F，E分别为AD、PC的中点．

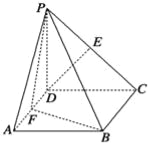
（1）证明：DE∥平面PFB；

（2）求三棱锥A﹣PFB的体积．

【答案】（1）详见解析；（2）.

【解析】

试题分析：(1)要证明线面平行，可先转化为证明线线平行，即构成平行四边形，取中点,连接，可证明四边形是平行四边形，从而证明出,根据线线平行，可证明线面平行；（2）.

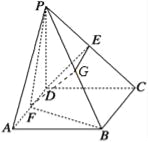
试题解析：解（1）取PB中点G，连接EG，FG，∵E，G分别是PC，PB的中点，∴EG∥BC，，∵DF∥，∴EG∥DF，EG=DF．

∴四边形DEGF是平行四边形，∴DE∥FG，∵DE平面PFB，FG平面PFB∴DE∥平面PFB．

（2），

∴三棱锥A﹣PFB的体积V===．

练习册系列答案

相关题目

【题目】已知四棱锥的底面为直角梯形，，，底面，且，，是的中点.

（1）证明：面面；

（2）求与夹角的余弦值；

（3）求面与面所成二面角余弦值的大小.

【题目】如图，平面平面，其中为矩形，为直角三角形，，.

（1）求证：平面平面；

（2）求直线与平面所成角的正弦值.

【题目】若a=log0.50.2，b=log20.2，c=20.2，则a，b，c的大小关系是（　　）

A. a＜b＜c B. b＜c＜a C. b＜a＜c D. c＜b＜a

【题目】已知函数是定义在上的偶函数，且当时，．

（1）现已画出函数在轴左侧的图象，如图所示，请补出完整函数的图象，并根据图象写出函数的增区间；

（2）写出函数的解析式和值域．

【题目】某细胞分裂时，由1个分裂成2个，2个分裂成4个，…，这样细胞分裂x次后，得到细胞总数y与x的函数关系是(　　)

A. y＝2x＋1－1(x∈N*) B. y＝2x(x∈N*)

C. y＝2x－1(x∈N*) D. y＝2x＋1(x∈N*)

【题目】若a>0, b>0, 且函数f(x)=4x3-ax2-2bx+2在x=1处有极值，则ab的最大值等于( )

A. 2 B. 3 C. 6 D. 9

【题目】某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参加其中一组．在参加活动的职工中，青年人占42.5%，中年人占47.5%，老年人占10%.登山组的职工占参加活动总人数的，且该组中青年人占50%，中年人占40%，老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度，现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本．试确定：

(1)游泳组中，青年人、中年人、老年人分别所占的比例；

(2)游泳组中，青年人、中年人、老年人分别应抽取的人数．

【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100 名电视观众,相关的数据如下表(单位:人)所示:

	收看文艺节目	收看新闻节目	总计
20至40岁	40	18	58
大于40岁	15	27	42
总计	55	45	100

由表中数据直观分析,收看新闻节目的观众是否与年龄有关:__________.（填“是”或“否”）

试题分类