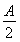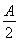题目内容
已知函数f(x)＝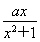
＋a，g(x)＝aln x－x(a≠0)．
(1)求函数f(x)的单调区间；
(2)求证：当a>0时，对于任意x1，x2∈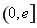
，总有g(x1)<f(x2)成立．
（1）当a>0时，f(x)的单调递增区间为(－1，1)，单调递减区间为(－∞，－1)，(1，＋∞)；当a<0时，f(x)的单调递增区间为(－∞，－1)，(1，＋∞)，单调递减区间为(－1，1)．（2）见解析
【解析】(1)函数f(x)的定义域为R，
f′(x)＝
.
当a>0时，当x变化时，f′(x)，f(x)的变化情况如下表：
x | (－∞，－1) | －1 | (－1，1) | 1 | (1，＋∞) |
f′(x) | － | 0 | ＋ | 0 | － |
f(x) | ↘ |
| ↗ |
| ↘ |
当a<0时，当x变化时，f′(x)，f(x)的变化情况如下表：
x | (－∞，－1) | －1 | (－1，1) | 1 | (1，＋∞) |
f′(x) | ＋ | 0 | － | 0 | ＋ |
f(x) | ↗ |
| ↘ |
| ↗ |
综上所述，当a>0时，f(x)的单调递增区间为(－1，1)，单调递减区间为(－∞，－1)，(1，＋∞)；当a<0时，f(x)的单调递增区间为(－∞，－1)，(1，＋∞)，单调递减区间为(－1，1)．
(2)证明：由(1)可知，当a>0时，f(x)在(0，1)上单调递增，f(x)在(1，e]上单调递减，且f(e)＝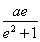
＋a>a＝f(0)．
所以x∈(0，e]时，f(x)>f(0)＝a.
因为g(x)＝aln x－x，所以g′(x)＝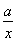
－1，
令g′(x)＝0，得x＝a.
①当0<a<e时，由g′(x)>0，得0<x<a；由g′(x)<0，得x>a，所以函数g(x)在(0，a)上单调递增，在(a，e]上单调递减，
所以g(x)max＝g(a)＝aln a－a.
因为a－(aln a－a)＝a(2－ln a)>a(2－ln e)＝a>0，
所以对于任意x1，x2∈(0，e]，总有g(x1)<f(x2)．
②当a≥e时，g′(x)≥0在(0，e]上恒成立，
所以函数g(x)在(0，e]上单调递增，g(x)max＝g(e)＝a－e<a，
所以对于任意x1，x2∈(0，e]，仍有g(x1)<f(x2)．
综上所述，对于任意x1，x2∈(0，e]，总有g(x1)<f(x2)．
