题目内容
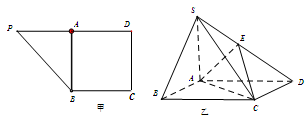
已知直角梯形 ,
,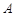 是
是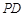 边上的中点(如图甲),
边上的中点(如图甲),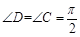 ,
,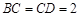 ,
,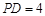 ,将
,将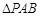 沿
沿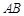 折到
折到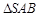 的位置,使
的位置,使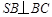 ,点
,点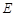 在
在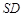 上,且
上,且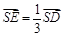 (如图乙)
(如图乙)
(Ⅰ)求证: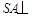 平面ABCD.
平面ABCD.
(Ⅱ)求二面角E?AC?D的余弦值
 ,
,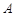 是
是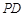 边上的中点(如图甲),
边上的中点(如图甲),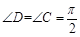 ,
,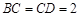 ,
,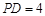 ,将
,将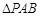 沿
沿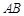 折到
折到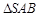 的位置,使
的位置,使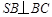 ,点
,点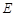 在
在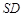 上,且
上,且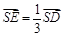 (如图乙)
(如图乙)
(Ⅰ)求证:
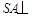 平面ABCD.
平面ABCD. (Ⅱ)求二面角E?AC?D的余弦值
(Ⅰ)见详解;(Ⅱ)

试题分析:先证
 ,且
,且 ,
,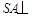 平面ABCD;根据几何法或向量法求出二面角E?AC?D的余弦值.
平面ABCD;根据几何法或向量法求出二面角E?AC?D的余弦值.试题解析:
(Ⅰ)证明:在题图中,由题意可知,
 ,ABCD为正方形,所以在图中,
,ABCD为正方形,所以在图中, ,
,四边形ABCD是边长为2的正方形,
因为
 ,且
,且 ,
,所以
 平面SAB, (3分)
平面SAB, (3分)又
 平面SAB,所以
平面SAB,所以 ,且
,且 ,
,所以
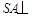 平面ABCD. (6分)
平面ABCD. (6分)(Ⅱ)解:方法一: 如图,在AD上取一点O,使
 ,连接EO.
,连接EO.
因为
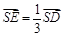 ,所以EO//SA , (7分)
,所以EO//SA , (7分)所以
 平面ABCD,过O作
平面ABCD,过O作 于H,连接EH,
于H,连接EH,则
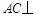 平面EOH,所以
平面EOH,所以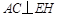 .
.所以
 为二面角E?AC?D的平面角, (9分)
为二面角E?AC?D的平面角, (9分) . 在Rt△AHO中,
. 在Rt△AHO中, . (11分)
. (11分)所以二面角E?AC?D的余弦值为
 . (12分)
. (12分)方法二:以A为原点建立空间直角坐标系,如图,


 , (7分)
, (7分)易知平面ACD的法向量为
 ,
,设平面EAC的法向量为
 ,
, , (9分)
, (9分)由
 所以
所以 可取
可取
所以
 , (11分)
, (11分)所以
 ,
,所以二面角E?AC?D的余弦值为
 . (12分)
. (12分)
练习册系列答案
相关题目
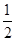 ,AD=1.
,AD=1.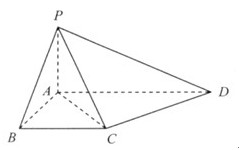
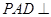 平面
平面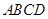 ,
,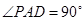 ,且
,且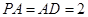 ,
, 、
、 、
、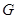 分别是线段
分别是线段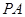 、
、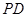 、
、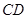 的中点.
的中点.
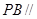 平面
平面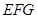 ;
;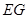 、
、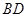 所成角的余弦值.
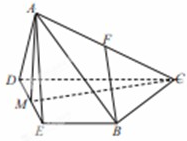
所成角的余弦值. 中,侧面
中,侧面 是等边三角形,在底面等腰梯形
是等边三角形,在底面等腰梯形 中,
中, ,
, ,
, ,
, ,
, 为
为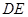 的中点,
的中点, 为
为 的中点,
的中点, .
.
 平面
平面 ;
; 平面
平面 .
.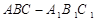 的底面是直角三角形,
的底面是直角三角形, 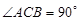 ,侧棱与底面所成角为
,侧棱与底面所成角为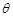 ,点
,点 在底面上的射影
在底面上的射影 落在
落在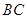 上.
上.
 平面
平面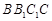 ;
;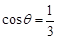 ,且当
,且当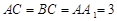 时,求二面角
时,求二面角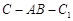 的大小.
的大小. =
= =90°
=90° =1200,AD=AB=1,AC交BD于 O 点.
=1200,AD=AB=1,AC交BD于 O 点.
 的正方形,剪去阴影部分后,得到圆锥的侧面和底面的展开图,则圆锥的体积是( ).
的正方形,剪去阴影部分后,得到圆锥的侧面和底面的展开图,则圆锥的体积是( ).




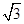
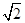
 的边长为6,
的边长为6, ,
, .将菱形
.将菱形 折起,得到三棱锥 ,点
折起,得到三棱锥 ,点 是棱
是棱 的中点,
的中点, .
.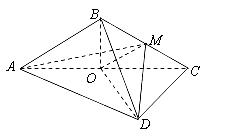
 ;
; 的体积.
的体积.