题目内容
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=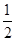 ,AD=1.
,AD=1.
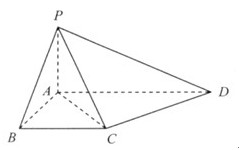
(I)求证:CD⊥平面PAC;
(II)求二面角A-PD-C的余弦值.
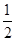 ,AD=1.
,AD=1.
(I)求证:CD⊥平面PAC;
(II)求二面角A-PD-C的余弦值.
(I)见解析;(II)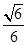 .
.
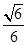 .
.试题分析:(I)先根据已知条件证明
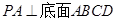 ,那么就有
,那么就有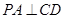 ,在根据题中已知边的长度,由勾股定理证明
,在根据题中已知边的长度,由勾股定理证明 ,根据直线与平面垂直的判定定理即可证明
,根据直线与平面垂直的判定定理即可证明 ;(II)设
;(II)设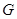 为
为 中点,连结
中点,连结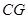 ,过
,过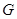 作
作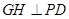 于
于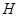 ,证明
,证明 是二面角
是二面角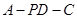 的平面角.再由
的平面角.再由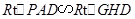 ,解得
,解得 和
和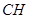 的值,求
的值,求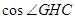 的余弦值即可.
的余弦值即可.试题解析:(I)∵
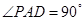 ,∴
,∴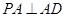 .
.又∵
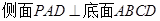 ,
, ,且
,且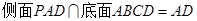 ,
,∴
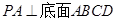 .
. 又
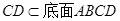 ,∴
,∴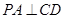 . 3分
. 3分在底面
 中,∵
中,∵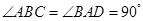 ,
, ,
,∴
 ,有
,有 ,∴
,∴ .
.又∵
 , ∴
, ∴ . 6分
. 6分(II)设
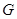 为
为 中点,连结
中点,连结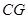 ,则
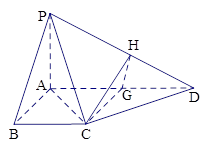
,则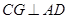 .
.
又∵
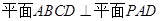 ,
,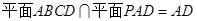 ,
,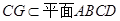 ,∴
,∴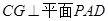 .
.∵
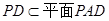 ,∴
,∴ .
.过
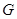 作
作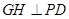 于
于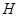 ,
,∵
 ,∴
,∴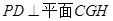 ,
,∴
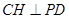 ,∴
,∴ 是二面角
是二面角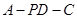 的平面角. 9分
的平面角. 9分由已知得
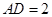 ,
,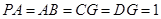 , ∴
, ∴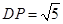 .
.由
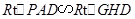 得,
得,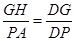 ,∴
,∴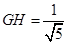 ,
,∴
 ,
,∴
 .
.即二面角
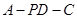 的余弦值为
的余弦值为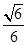 . 12分
. 12分
练习册系列答案
相关题目
 中,
中,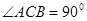 ,
, ,
, ,在三角形内挖去一个半圆(圆心
,在三角形内挖去一个半圆(圆心 在边
在边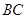 上,半圆与
上,半圆与 、
、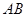 分别相切于点
分别相切于点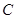 、
、 ,与
,与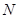 ),将△
),将△
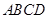 中,
中, ,
, ,将矩形沿对角线
,将矩形沿对角线 把
把 折起,使
折起,使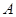 移到
移到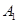 点,且
点,且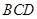 上的射影
上的射影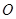 恰好在
恰好在 上.
上.
 ;
; 平面
平面 ;
; 的余弦值.
的余弦值. ,
, 是
是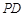 边上的中点(如图甲),
边上的中点(如图甲),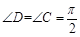 ,
,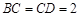 ,
,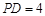 ,将
,将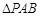 沿
沿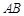 折到
折到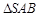 的位置,使
的位置,使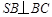 ,点
,点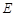 在
在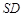 上,且
上,且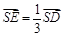 (如图乙)
(如图乙)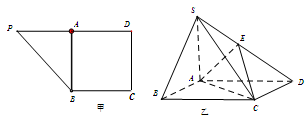
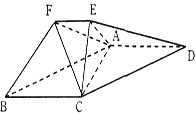
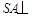 平面ABCD.
平面ABCD. 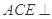 平面
平面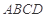 ,四边形
,四边形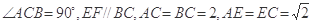 .
.
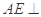 平面
平面 ;
;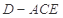 的体积.
的体积.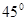 ,腰和上底均为1的等腰梯形,则这个平面图形的面积( )
,腰和上底均为1的等腰梯形,则这个平面图形的面积( )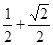
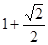
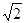
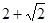
 中(图1),
中(图1), ,
,
 中点为
中点为 ,将图1沿直线
,将图1沿直线 为
为 (图2)
(图2)

 作直线
作直线 平面
平面 ,且
,且 平面
平面 ,求
,求 的长度。
的长度。 与平面
与平面 所成角的正弦值。
所成角的正弦值。 的各个顶点都在表面积为
的各个顶点都在表面积为 的球
的球 的球面上,其中
的球面上,其中 ,则四棱锥
,则四棱锥 的体积为( )
的体积为( )


