题目内容
一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A.2 | B.3 | C.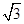 | D.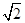 |
D
试题分析:设球的半径为
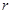 ,由正四面体的体积得:
,由正四面体的体积得: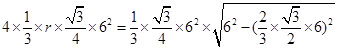 ,
,所以
 ,设正方体的最大棱长为
,设正方体的最大棱长为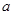 ,∴
,∴ ,∴
,∴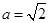 .
.
练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
题目内容
| A.2 | B.3 | C.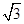 | D.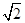 |
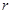 ,由正四面体的体积得:
,由正四面体的体积得: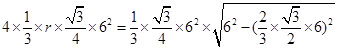 ,
, ,设正方体的最大棱长为
,设正方体的最大棱长为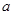 ,∴
,∴ ,∴
,∴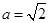 .
.
 高效智能课时作业系列答案
高效智能课时作业系列答案