题目内容
【题目】已知各项均为正数的数列{an}的首项a1=1,Sn是数列{an}的前n项和,且满足:anSn+1﹣an+1Sn+an﹣an+1= ![]() anan+1 , 则
anan+1 , 则 ![]() S12= .
S12= .
【答案】3
【解析】解:∵anSn+1﹣an+1Sn+an﹣an+1= ![]() anan+1 , 且Sn+1=Sn+an+1 , ∴(an﹣an+1)Sn+
anan+1 , 且Sn+1=Sn+an+1 , ∴(an﹣an+1)Sn+ ![]() anan+1+an﹣an+1=0,
anan+1+an﹣an+1=0,
∴Sn+ ![]() +1=0;
+1=0;
又∵a1=1,令n=1,则1+ ![]() +1=0,解得a2=
+1=0,解得a2= ![]() ,
,
同理可得a3= ![]() ,
,
猜想an= ![]() ;
;
下面利用数学归纳法证明:
② 当n=1时,a1= ![]() =1,成立;
=1,成立;
②假设当n≤k(k∈N*)时成立,ak= ![]() ,则Sk=
,则Sk= ![]() =
= ![]() ;
;
∵Sk+ ![]() +1=0,
+1=0,
∴ ![]() +
+ 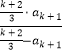 +1=0,
+1=0,
解得ak+1= ![]() ;
;
因此当n=k+1时也成立,
综上,对于n∈N* , an= ![]() 都成立;
都成立;
由等差数列的前n项和公式得,Sn= ![]() ;
;
∴ ![]() S12=
S12= ![]() ×
× ![]() =3.
=3.
【考点精析】关于本题考查的等比数列的通项公式(及其变式)和等比数列的前n项和公式,需要了解通项公式:![]() ;前
;前![]() 项和公式:
项和公式: 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目