题目内容
((本小题满分13分)设O为坐标原点,曲线x2+y2+2x-6y+1=0上有两点P、Q关于直线x+my+4=0对称,又满足OP⊥OQ.
(1)求m的值;
(2)求直线PQ的方程.
(1)求m的值;
(2)求直线PQ的方程.
解: (1)曲线方程可化为(x+1)2+(y-3)2=9,是圆心为(-1,3),半径为3的圆.
因为点P,Q在圆上且关于直线x+my+4=0对称,
所以圆心(-1,3)在直线x+my+4=0上,代入得m=-1.
(2)因为直线PQ与直线y=x+4垂直,所以设 P(x1,y1),Q(x2,y2)
则直线PQ的方程为y=-x+b.将直线y=-x+b代入圆的方程,得2x2+2(4-b)x+b2-6b+1=0,Δ=4(4-b)2-4×2(b2-6b+1)>0,解得2-3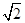 <b<2+3
<b<2+3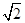 .
.
x1+x2=b-4,x1x2=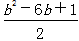 ,
,
y1y2=(-x1+b)(-x2+b)=b2-b(x1+x2)+x1x2=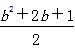 ,
,
因为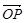 ·
·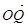 =0,所以x1x2+y1y2=0,
=0,所以x1x2+y1y2=0,
即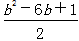 +
+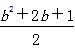 =0,得b=1.
=0,得b=1.
故所求的直线方程为y=-x+1.

因为点P,Q在圆上且关于直线x+my+4=0对称,
所以圆心(-1,3)在直线x+my+4=0上,代入得m=-1.
(2)因为直线PQ与直线y=x+4垂直,所以设 P(x1,y1),Q(x2,y2)
则直线PQ的方程为y=-x+b.将直线y=-x+b代入圆的方程,得2x2+2(4-b)x+b2-6b+1=0,Δ=4(4-b)2-4×2(b2-6b+1)>0,解得2-3
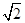 <b<2+3
<b<2+3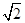 .
.x1+x2=b-4,x1x2=
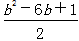 ,
,y1y2=(-x1+b)(-x2+b)=b2-b(x1+x2)+x1x2=
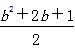 ,
,因为
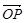 ·
·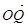 =0,所以x1x2+y1y2=0,
=0,所以x1x2+y1y2=0,即
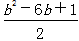 +
+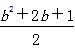 =0,得b=1.
=0,得b=1.故所求的直线方程为y=-x+1.
略

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 若x≥0,则动点
若x≥0,则动点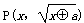 的轨迹是
的轨迹是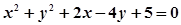 的圆心.
的圆心.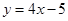 的距离最短,并求距离的最小值.
的距离最短,并求距离的最小值. 与抛物线
与抛物线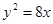 交于不同两点
交于不同两点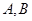 ,若线段
,若线段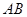 中点的纵坐标为
中点的纵坐标为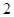 ,则
,则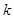 等于( )
等于( )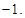
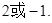
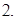
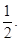
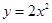 的准线方程( )
的准线方程( )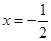 .
. 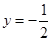 .
. 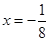 .
. .
.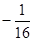 )
)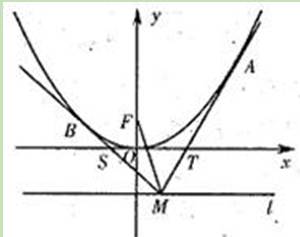
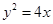 上的两点A、B满足
上的两点A、B满足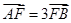 ,则弦AB的中点到准线的距离为 。
,则弦AB的中点到准线的距离为 。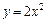 的焦点坐标是 。
的焦点坐标是 。