题目内容
【题目】已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点. (Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设 ![]() ,
, ![]() ,求证λ+μ为定值.
,求证λ+μ为定值.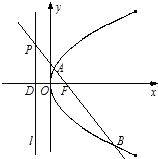
【答案】解:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0), 于是直线PF的斜率为 ![]() ,
,
所以直线PF的方程为 ![]() ,即为mx+2y﹣m=0.
,即为mx+2y﹣m=0.
(Ⅱ)设A,B两点的坐标分别为(x1 , y1),(x2 , y2),
由 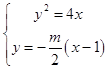 得m2x2﹣(2m2+16)x+m2=0,
得m2x2﹣(2m2+16)x+m2=0,
所以 ![]() ,x1x2=1.
,x1x2=1.
于是 ![]() .
.
点D到直线mx+2y﹣m=0的距离 ![]() ,
,
所以 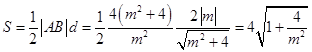 .
.
因为m∈R且m≠0,于是S>4,
所以△DAB的面积S范围是(4,+∞).
(Ⅲ)由(Ⅱ)及 ![]() ,
, ![]() ,得(1﹣x1 , ﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1 , m﹣y1)=μ(x2+1,y2﹣m),
,得(1﹣x1 , ﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1 , m﹣y1)=μ(x2+1,y2﹣m),
于是 ![]() ,
, ![]() (x2≠±1).
(x2≠±1).
所以 ![]() .
.
所以λ+μ为定值0
【解析】(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),求出斜率用点斜式写出直线方程.(Ⅱ)设A,B两点的坐标分别为(x1 , y1),(x2 , y2),用弦长公式求出线段AB的长,再由点到直线的距离公式求点D到直线AB的距离,用三角形面积公式表示出面积关于参数m的表达式,再根据m的取值范围求出面积的范围.(Ⅲ) ![]() ,
, ![]() ,变化为坐标表示式,从中求出参数λ,μ用两点A,B的坐标表示的表达式,即可证明出两者之和为定值.
,变化为坐标表示式,从中求出参数λ,μ用两点A,B的坐标表示的表达式,即可证明出两者之和为定值.
【考点精析】本题主要考查了一般式方程的相关知识点,需要掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0)才能正确解答此题.
(A,B不同时为0)才能正确解答此题.

练习册系列答案
相关题目