Question

【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果，结果有50个特等品.将这50个水果的质量数据分组，得到下边的频率分布表.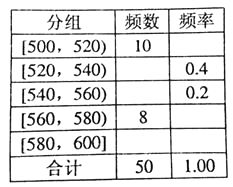

（1）估计该水果的质量不少于560g的概率；
（2）若在某批水果的检测中，发现有15个特等品，据此估计该批水果中没有达到特等品的个数.

Answer 1

【答案】
（1）解：由已知可得该水果的质量不少于560g的概率

p＝0.16＋0.04＝0.2

（2）解：设该批水果中没有达到特等品的个数为x，则有

，解得x＝285．

【解析】（1）根据频数=总数频率分别求出[520,540）、[540，560）两组的频数，然后根据频率=频数总数及频率之和等于1分别求出其余三组的频率，则根据P（不少于560g）=P（[560,580））+P（[580,600））即可求解；（2）设该批水果中没有达到特等品的个数为x，根据“特等品在样本中所占比例与其在总体中所占比例相等”列方程.
【考点精析】解答此题的关键在于理解频率分布表的相关知识，掌握第一步，求极差；第二步，决定组距与组数；第三步，确定分点，将数据分组；第四步，列频率分布表．