题目内容
某工厂建一个长方形无盖蓄水池,其容积为4800m3,深度为3m。如果池底每1 m2的造价为150元,池壁每1 m2的造价为120元,怎么设计水池能使造价最低?最低造价多少元?
297600
解析试题分析:水池呈长方形,它的高是3m,底面的长与宽没有确定;如果底面的长与宽确定了,水池的总造价也就确定了;可以设底面的长与宽分别为xm,ym,水池总造价为z元,建立函数关系式,求出z的最小值.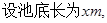
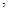 则宽为
则宽为 ,总造价为
,总造价为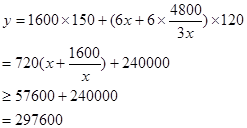
当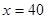 m时,等号成立。
m时,等号成立。
所以设计池底为40m,宽为40 m时,总造价最低位297600元。
考点:基本不等式在最值问题中的应用;函数的最值及其几何意义.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
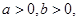 且
且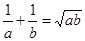
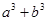 的最小值;
的最小值;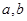 ,使得
,使得 ?并说明理由.
?并说明理由.
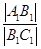 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;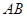 、
、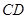 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知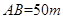 ,
,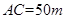 ,当
,当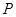 为
为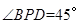 .
.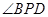 达到最大.
达到最大.
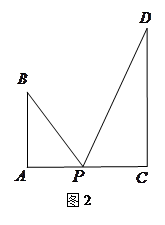
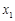 ,
, ,
,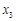 为正实数,若
为正实数,若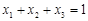 ,求证:
,求证: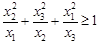 .
. (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
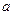 ≥0,
≥0, 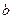 ≥0,
≥0, 则
则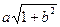 的最大值是_________.
的最大值是_________.