题目内容
(本题满分12分) 已知a,b都是正实数,且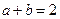 ,求证:
,求证: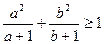
证明:因为a,b都是正实数,所以原不等式等价于 ,即
,即
等价于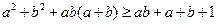 , ……6分
, ……6分
将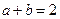 代入,只需要证明
代入,只需要证明 ,即
,即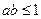
而由已知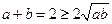 ,可得
,可得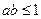 成立,所以原不等式成立。 ……12分
成立,所以原不等式成立。 ……12分
另证:因为a,b都是正实数,所以 ,
,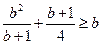 ……6分
……6分
两式相加得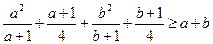 , ……8分
, ……8分
因为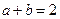 ,所以
,所以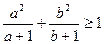 。 ……12分
。 ……12分
解析

练习册系列答案
相关题目
已知区域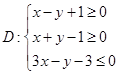 的面积为
的面积为 ,点集
,点集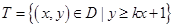 在坐标系中对应区域的面积为
在坐标系中对应区域的面积为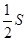 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
设 满足约束条件
满足约束条件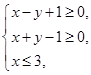 ,则
,则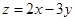 的最小值是( )
的最小值是( )
A.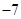 | B.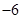 | C.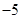 | D.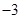 |
若变量 、
、 满足约束条件
满足约束条件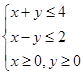 ,则
,则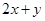 的最大值是( )
的最大值是( )
| A.2 | B.4 | C.7 | D.8 |
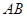 、
、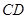 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知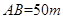 ,
,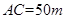 ,当
,当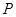 为
为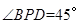 .
. 达到最大.
达到最大.
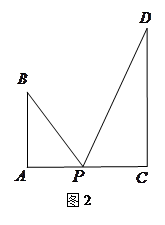
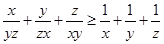 .
.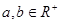 ,且
,且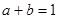 ,则
,则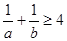 ;
;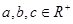 ,且
,且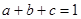 ,则
,则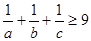 ;
;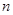 个正数
个正数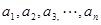 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。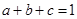 ,且
,且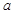 、
、 、
、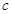 是正数,求证:
是正数,求证: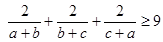 .
. (a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )
(a≠0)取得最大值时的最优解有无穷多组,则点(a,b)的轨迹可能是( )