题目内容
已知圆的方程x2+y2=25，则过点P（3，4）的圆的切线方程为（ ）
分析：由圆的方程找出圆心坐标和圆的半径，然后求出P与圆心的距离判断出P在圆上即P为切点，根据圆的切线垂直于过切点的直径，由圆心和M的坐标求出OP确定直线方程的斜率，根据两直线垂直时斜率乘积为-1，求出切线的斜率，根据P坐标和求出的斜率写出切线方程即可．
解答：解：由圆x2+y2=25，得到圆心A的坐标为（0，0），圆的半径r=5，
而|AP|=5=r，所以P在圆上，则过P作圆的切线与AP所在的直线垂直，
又P（3，4），得到AP所在直线的斜率为-
，所以切线的斜率为
，
则切线方程为：y-4=
（x-3）即3x+4y-25=0．
故选C．
而|AP|=5=r，所以P在圆上，则过P作圆的切线与AP所在的直线垂直，
又P（3，4），得到AP所在直线的斜率为-
| 4 |
| 3 |
| 3 |
| 4 |
则切线方程为：y-4=
| 3 |
| 4 |
故选C．
点评：此题考查学生掌握点与圆的位置关系及直线与圆的位置关系，掌握两直线垂直时斜率所满足的关系，会根据一点的坐标和直线的斜率写出直线的方程，是一道综合题．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知圆的方程x2+y2=25，过M（-4，3）作直线MA，MB与圆交于点A，B，且MA，MB关于直线y=3对称，则直线AB的斜率等于（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
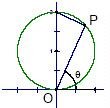已知圆的方程x2+（y-1）2=1，P为圆上任意一点（不包括原点）．直线OP的倾斜角为θ弧度，|OP|=d，则d=f（θ）的图象大致为已知圆的方程x2+y2=4，若抛物线过点A（0，-1），B（0，1）且以圆的切线为准线，则抛物线的焦点轨迹方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|