题目内容
已知圆的方程x2+y2=4,若抛物线过点A(0,-1),B(0,1)且以圆的切线为准线,则抛物线的焦点轨迹方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:设出切线方程,表示出圆心到切线的距离求得a和b的关系,设出焦点坐标,根据抛物线的定义求得点A,B到准线的距离等于其到焦点的距离,然后两式平方后分别相加和相减,联立后求得x和y的关系式.
解答:解:设切线ax+by-1=0,圆心到切线距离等于半径
=2
∴
=
,∴a2+b2=
设焦点(x,y),抛物线定义,
=
=
平方相加得:2x2+2+2y2=8(a2+1)
相减得:4y=16a,a=
所以2x2+2+2y2=8(
+1)
即:
+
=1
依题意焦点不能与A,B共线
∴x≠0
故抛物线的焦点轨迹方程为
+
=1(x≠0)
故选C
| 1 | ||
|
∴
| a2+b2 |
| 1 |
| 2 |
| 1 |
| 4 |
设焦点(x,y),抛物线定义,
| (y+1)2+x2 |
| |-a-1| | ||
|
| (y-1)2+x2 |
| |a-1| | ||
|
平方相加得:2x2+2+2y2=8(a2+1)
相减得:4y=16a,a=
| y |
| 4 |
所以2x2+2+2y2=8(
| y2 |
| 16 |
即:
| x2 |
| 3 |
| y2 |
| 4 |
依题意焦点不能与A,B共线
∴x≠0
故抛物线的焦点轨迹方程为
| x2 |
| 3 |
| y2 |
| 4 |
故选C
点评:本题主要考查了椭圆的标准方程.考查了学生数形结合的思想及综合分析问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知圆的方程x2+y2=25,过M(-4,3)作直线MA,MB与圆交于点A,B,且MA,MB关于直线y=3对称,则直线AB的斜率等于( )
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
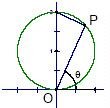 已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为
已知圆的方程x2+(y-1)2=1,P为圆上任意一点(不包括原点).直线OP的倾斜角为θ弧度,|OP|=d,则d=f(θ)的图象大致为