题目内容
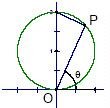已知圆的方程x2+（y-1）2=1，P为圆上任意一点（不包括原点）．直线OP的倾斜角为θ弧度，|OP|=d，则d=f（θ）的图象大致为分析：由图形可以看出，可以在OP与直径围成的三角形中通过解三角形求出d与θ的函数关系，再根据函数表达式作出图象即可．
解答：解：在直角三角形中，因直径的长度为2，其所邻的角为
-θ故
|OP|=2cos(
-θ)=2sinθ，θ∈(0，π)
故函数图象为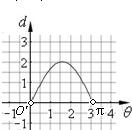
故应填．
| π |
| 2 |
|OP|=2cos(
| π |
| 2 |
故函数图象为
故应填
．点评：本题考点是直线与圆的位置关系，在圆中考查三角函数，是本题的一大亮点，新颖．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
已知圆的方程x2+y2=25，过M（-4，3）作直线MA，MB与圆交于点A，B，且MA，MB关于直线y=3对称，则直线AB的斜率等于（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知圆的方程x2+y2=4，若抛物线过点A（0，-1），B（0，1）且以圆的切线为准线，则抛物线的焦点轨迹方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|