题目内容
已知点P(x,y)在约束条件
|
分析:本题考查的知识点是几何概型的意义,关键是要找出(x,y)对应图形的面积,及满足条件“(x-2)2+(y-2)2≤4”的点对应的图形的面积,然后再结合几何概型的计算公式进行求解.
解答: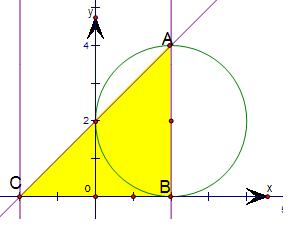 解:如图所示,区域Ω为图中阴影部分的三角形,其面积为:
解:如图所示,区域Ω为图中阴影部分的三角形,其面积为:
× 4×4=8,
条件“(x-2)2+(y-2)2≤4”的点对应的图形是图中阴影部分内的圆的部分,其面积为:π+2.
则所求的概率P=
故答案为:
.
 解:如图所示,区域Ω为图中阴影部分的三角形,其面积为:
解:如图所示,区域Ω为图中阴影部分的三角形,其面积为:| 1 |
| 2 |
条件“(x-2)2+(y-2)2≤4”的点对应的图形是图中阴影部分内的圆的部分,其面积为:π+2.
则所求的概率P=
| π+2 |
| 8 |
故答案为:
| π+2 |
| 8 |
点评:本题考查的知识点是几何概型的意义,简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目