题目内容
设椭圆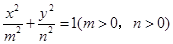 的右焦点为
的右焦点为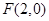 ,离心率为
,离心率为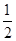 ,则此椭圆的方程为___________
,则此椭圆的方程为___________
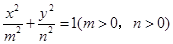 的右焦点为
的右焦点为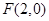 ,离心率为
,离心率为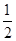 ,则此椭圆的方程为___________
,则此椭圆的方程为___________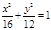
此题考查椭圆的性质
思路分析:因为椭圆右焦点为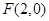 所以
所以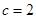 ,又离心率为
,又离心率为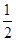 ,故
,故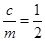 ,
, ,因此
,因此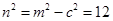 ,故椭圆方程为
,故椭圆方程为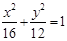 .
.
思路分析:因为椭圆右焦点为
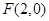 所以
所以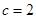 ,又离心率为
,又离心率为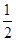 ,故
,故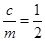 ,
, ,因此
,因此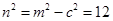 ,故椭圆方程为
,故椭圆方程为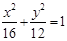 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
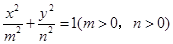 的右焦点为
的右焦点为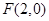 ,离心率为
,离心率为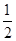 ,则此椭圆的方程为___________
,则此椭圆的方程为___________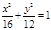
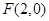 所以
所以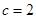 ,又离心率为
,又离心率为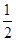 ,故
,故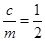 ,
, ,因此
,因此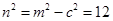 ,故椭圆方程为
,故椭圆方程为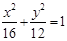 .
.
 阅读快车系列答案
阅读快车系列答案