题目内容
设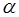 ∈(0,
∈(0,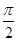 ),方程
),方程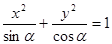 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则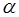 的取值范围是( )
的取值范围是( )
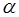 ∈(0,
∈(0,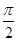 ),方程
),方程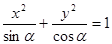 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则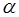 的取值范围是( )
的取值范围是( )A.(0,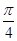 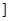 | B.(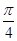 , ,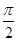 ) ) | C.(0,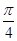 ) ) | D.[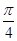 , ,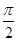 ) ) |
B
依题意可得,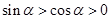 。因为
。因为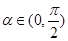 ,所以
,所以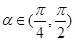 ,故选B
,故选B
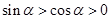 。因为
。因为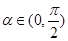 ,所以
,所以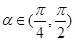 ,故选B
,故选B
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
题目内容
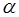 ∈(0,
∈(0,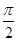 ),方程
),方程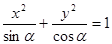 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则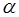 的取值范围是( )
的取值范围是( )A.(0,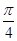 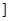 | B.(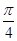 , ,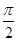 ) ) | C.(0,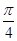 ) ) | D.[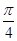 , ,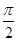 ) ) |
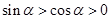 。因为
。因为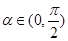 ,所以
,所以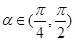 ,故选B
,故选B
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案