题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,试讨论函数
时,试讨论函数![]() 的单调性,并求出函数
的单调性,并求出函数![]() 的极值;
的极值;
(2)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)①当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增, ![]() 无极值,②当
无极值,②当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减, ![]() 的极大值
的极大值![]() ,
, ![]() 无极小值(2)
无极小值(2)![]()
【解析】
(1)求出导数,分![]() ,
,![]() 两类讨论求函数的单调区间及极值(2)原不等式恒成立转化为
两类讨论求函数的单调区间及极值(2)原不等式恒成立转化为![]() 恒成立,对
恒成立,对![]() 求导数,分
求导数,分![]() ,
,![]() 两种情况讨论,求出最小值
两种情况讨论,求出最小值![]() ,可得
,可得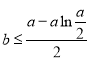 ,构造函数
,构造函数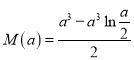 ,利用导数求最大值即可.
,利用导数求最大值即可.
(1)![]()
①当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 无极值
无极值
②当![]() 时,
时,![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,且
,且![]() 无极小值
无极小值
(2)![]() ,
,![]() .
.
若![]() ,由
,由![]() 知
知![]() ,取
,取![]() ,使得
,使得![]() ,
,
则![]() ,而
,而![]() ,
,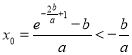
所以![]() ,所以
,所以![]() ,与
,与![]() 矛盾
矛盾
故![]() ,且
,且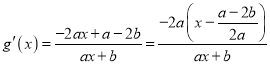 ,
,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
因此![]() ,故
,故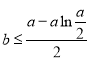
所以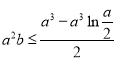
记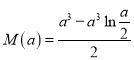 ,则
,则![]() ,则
,则![]() 在
在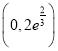 上单调递增,在
上单调递增,在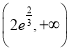 上单调递减,因此
上单调递减,因此 ,
,
所以当![]() ,
,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个