题目内容
已知椭圆 的离心率为
的离心率为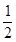 ,其左焦点
,其左焦点 到点
到点 的距离为
的距离为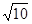 .
.
(1)求椭圆的方程;
(2)过右焦点 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点 、
、 ,则
,则 内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
【答案】
(1) ;(2)圆的面积的最大值为
;(2)圆的面积的最大值为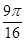 ,直线方程
,直线方程 .
.
【解析】
试题分析:本题考查椭圆的方程,直线与椭圆的位置关系及研究三角形内切圆面积问题.(1)由椭圆的离心率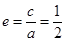 和左焦点
和左焦点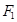 到点
到点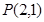 的距离为
的距离为 ,建立方程组,求出
,建立方程组,求出 、
、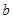 的值,从而得出椭圆方程;(2)是探索性问题,研究是否存在过椭圆的右焦点
的值,从而得出椭圆方程;(2)是探索性问题,研究是否存在过椭圆的右焦点 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点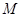 、
、 ,使得
,使得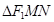 内切圆的圆面积最大的问题,求解分三个步骤,根据条件得出
内切圆的圆面积最大的问题,求解分三个步骤,根据条件得出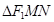 面积的关系式,将
面积的关系式,将 用直线
用直线 的斜率的倒数表示,再通过函数知识求面积的最大值;由此求出直线
的斜率的倒数表示,再通过函数知识求面积的最大值;由此求出直线 的方程;将由面积关系式
的方程;将由面积关系式 得到的面积的最大值代入面积关系式
得到的面积的最大值代入面积关系式 ,即可得到圆的半径的最大值,进而求出圆的面积的最大值.
,即可得到圆的半径的最大值,进而求出圆的面积的最大值.
试题解析:(1)设椭圆左焦点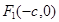 ,则
,则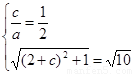 ,解得
,解得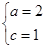 ,
,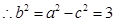 ,
,
故所求椭圆方程为 .
.
(2)设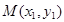 ,
,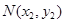 ,令
,令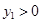 ,
,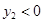 ,设
,设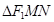 的内切圆的半径为
的内切圆的半径为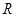 ,则
,则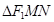 的周长为
的周长为 ,
,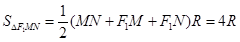 ,
,
因此若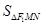 最大,则
最大,则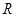 最大,
最大,
又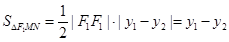 ,由题设知直线
,由题设知直线 的斜率不为0,可设直线
的斜率不为0,可设直线 的方程为
的方程为 ,
,
联立方程组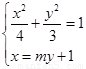 消去
消去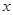 整理得
整理得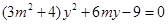 ,
,
由根与系数的关系得 ,
, ,
,
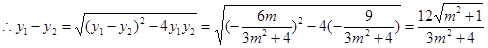 ,
,
即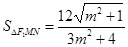 ,令
,令 ,则
,则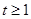 ,由此得
,由此得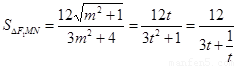 ,
,
令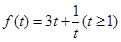 ,即
,即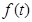 在
在 上单调递增,
上单调递增,
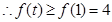 ,则
,则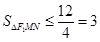 (当且仅当
(当且仅当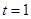 时,
时,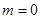 ,
,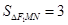 ),
),
这时所求内切圆的面积的最大值为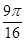 ,
,
故直线 的方程为
的方程为 ,
,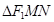 内切圆的面积的最大值为
内切圆的面积的最大值为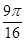 .
.
考点:椭圆方程,直线与椭圆的位置关系,三角形的内切圆面积.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
,焦点是(-3,0),(3,0),则椭圆方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C: 如图,A,B是椭圆C:
如图,A,B是椭圆C: