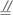题目内容
如图三棱锥A-BCD中，截面四边形EFGH是梯形，其中EF∥GH，点E，F，G，H分别在AB、BC、CD、DA上；（1）求证：EH、FG、BD三条直线交于同一点；
（2）求证：AC∥平面EFGH．
分析：（1）先证P为两个平面的公共点，利用两个平面的公共点在两个平面的公共直线上，证线共点；
（2）由EF∥GH，得EF∥平面ACD，得AC∥EF，再得线面平行．
（2）由EF∥GH，得EF∥平面ACD，得AC∥EF，再得线面平行．
解答：
证明：（1）∵点E，F，G，H分别在AB、BC、CD、DA上，∴EH?平面ABD，FG?平面BCD，
∵EH∩FG=P，平面ABD∩平面BCD=BD，∴P∈BD，
即EH、FG、BD三条直线交于点P；
（2）∵EF∥GH，GH?平面ACD，EF?平面ACD，∴EF∥平面ACD，EF?平面ABC，
平面ABC∩平面ACD=AC，∴AC∥EF，又EF?平面EFGH，AC?平面EFGH，
∴AC∥平面EFGH．
证明：（1）∵点E，F，G，H分别在AB、BC、CD、DA上，∴EH?平面ABD，FG?平面BCD，∵EH∩FG=P，平面ABD∩平面BCD=BD，∴P∈BD，
即EH、FG、BD三条直线交于点P；
（2）∵EF∥GH，GH?平面ACD，EF?平面ACD，∴EF∥平面ACD，EF?平面ABC，
平面ABC∩平面ACD=AC，∴AC∥EF，又EF?平面EFGH，AC?平面EFGH，
∴AC∥平面EFGH．
点评：本题考查了用公理2证明点共线问题，考查平行关系的转化，考查了学生的空间想象能力和推理论证能力，本题较好的体现了线线、线面平行关系的转化．
练习册系列答案
相关题目
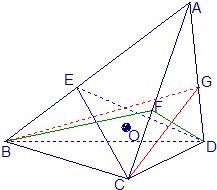如图，在体积为1的三棱锥A-BCD侧棱AB、AC、AD上分别取点E、F、G，使AE：EB=AF：FC=AG：GD=2：1，记O为三平面BCG、CDE、DBF的交点，则三棱锥O-BCD的体积等于（ ）
（2011•广州模拟）已知正方形ABCD的边长为2，AC∩BD=O．将正方形ABCD沿对角线BD折起，使AC=a，得到三棱锥A-BCD，如图所示． 
