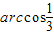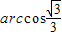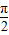题目内容
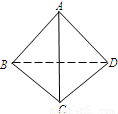
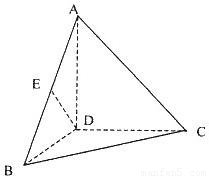
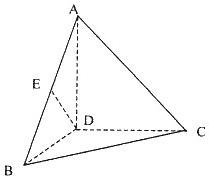 如图,四面体A-BCD中,AD⊥BD,AD⊥CD,BD⊥CD,且AD=BD=CD=2,点E是线段AB的中点.
如图,四面体A-BCD中,AD⊥BD,AD⊥CD,BD⊥CD,且AD=BD=CD=2,点E是线段AB的中点.(1)求证:DE是异面直线AB与CD的公垂线;
(2)求异面直线AB与CD间的距离;
(3)求异面直线DE与BC所成的角.
分析:以BD所在直线为x轴,以CD所在直线为y轴,以AD所在直线为z轴建系;并求出各点对应坐标;
(1)求出
,
,
的坐标,推出
•
=0以及
•
=0即可.
(2)根据
的坐标结合第一问的结论,直接代入两点间的距离公式即可求出结论;
(3)直接代入利用向量求两直线间的夹角公式即可.
(1)求出
| DE |
| AB |
| CD |
| AB |
| DE |
| DE |
| DC |
(2)根据
| DE |
(3)直接代入利用向量求两直线间的夹角公式即可.
解答: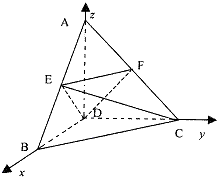 解:(1)以BD所在直线为x轴,以CD所在直线为y轴,以AD所在直线为z轴建系如图
解:(1)以BD所在直线为x轴,以CD所在直线为y轴,以AD所在直线为z轴建系如图
由题意知D(0,0,0),A(0,0,2),B(2,0,0),C(0,2,0),E(1,0,1)
∴
=(2,0,-2),
=(1,0,1),
=(0,2,0)
∴
•
=0,
•
=0.
∴AB⊥DE,DE⊥DC.
即DE是异面直线AB与CD的公垂线.
(2)|
|=
∴异面直线AB与CD间的距离是
.
(3)∵
=(-2,2,0)
∴
•
=-2,|
|=2
;
∴cosθ=
=
=-
.
∴θ=120°.
∴异面直线DE与BC所成的角为60°.
 解:(1)以BD所在直线为x轴,以CD所在直线为y轴,以AD所在直线为z轴建系如图
解:(1)以BD所在直线为x轴,以CD所在直线为y轴,以AD所在直线为z轴建系如图由题意知D(0,0,0),A(0,0,2),B(2,0,0),C(0,2,0),E(1,0,1)
∴
| AB |
| DE |
| DC |
∴
| AB |
| DE |
| DE |
| DC |
∴AB⊥DE,DE⊥DC.
即DE是异面直线AB与CD的公垂线.
(2)|
| DE |
| 2 |
∴异面直线AB与CD间的距离是
| 2 |
(3)∵
| BC |
∴
| BC |
| DE |
| BC |
| 2 |
∴cosθ=
| ||||
|
|
| -2 | ||||
2
|
| 1 |
| 2 |
∴θ=120°.
∴异面直线DE与BC所成的角为60°.
点评:本题主要考查空间向量在求夹角以及距离的应用问题.解决第三问时,一定要注意两异面直线所成角的范围是(0°,90°】,避免出错.

练习册系列答案
相关题目
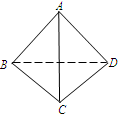 如图,四面体A-BCD的四个面全等,且AB=AC=
如图,四面体A-BCD的四个面全等,且AB=AC= 如图,四面体A-BCD的四个面全等,且AB=AC=
如图,四面体A-BCD的四个面全等,且AB=AC= ,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为
,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为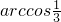
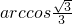


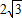 ,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为( )
,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为( )