Question

（2013•文昌模拟）如图，四边形OABC是边长为1的正方形，OD=3，点P为△BCD内（含边界）的动点，设

OP

=α

OC

+β

OD

（α，β∈R），则α+β的最大值等于 （　　）

• A．

  1

  4

• B．

  4

  3

• C．

  1

  3

• D．1

Answer 1

分析：先建立以O为原点，以OD所在直线为x轴的直角坐标系，根据条件求出点P的坐标与α，β之间的关系；再根据点P的位置，借助于可行域即可求解．

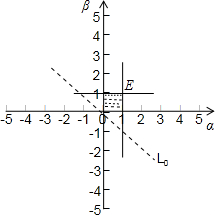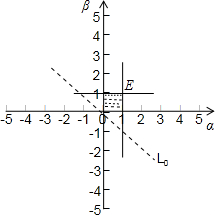解答：解：以O为原点，以OD所在直线为x轴建立直角坐标系，
点P（x，y），则（x，y）=α（0，1）+β（3，0）=（3β，α），
所以x=3β，y=α，α+β=y+

x

3

．
因为：0≤x=3β≤3，0≤y=α≤1⇒

0≤β≤1 0≤α≤1

设z=α+β，根据可行域知，
当点P为点E（1，1）时，α+β=z最大，其最大值为

4

3

，
故选B．

点评：本题主要考查相等向量以及线性规划的简单应用，是对知识点的综合考查，考查计算能力．